Attention Mechanism 시각화
2018년 7월 9일 초안 작성
본론
지난 번에는 시퀀스에 대한 모든 정보를 단일 벡터로 인코딩 한 다음 디코더가 이를 기반으로 결과를 추론하는 Seq2Seq 모델이 잘 동작함을 살펴보았다.
그러나, 입력 시퀀스가 매우 길 경우에는 장기 의존성long term dependencies 문제가 있다. 일반적으로 LSTM은 이 문제를 잘 처리 한다고 알려져 있지만 실제로는 여전히 문제가 있다. 이 때문에 입력 시퀀스를 뒤집을 경우 디코더에서 인코더의 관련 부분까지 경로를 단축하여, 보다 좋은 성능을 보여주기도 한다. (Sutskever et al., 2014)1 또한 입력 시퀀스를 두 번 반복하면 네트워크가 더 잘 기억memorize하는데 도움을 주기도 한다. (Zaremba, Sutskever, 2014)2
Attention
어텐션 메커니즘은 모델로 하여금 ‘중요한 부분만 집중attention하게 만들자’가 핵심 아이디어다.3 디코더가 출력을 생성할때 각 단계별로 입력 시퀀스의 각기 다른 부분을 집중하게 할 수 있게 한다. 즉, 하나의 고정된 컨텍스트 벡터로 인코딩 하는 대신 출력의 각 단계별로 컨텍스트 벡터를 생성하는 방법을 학습한다. 이는 모델이 입력 시퀀스와 지금까지 생성한 결과를 통해 무엇에 집중(!)할 것인지를 학습한다.4

Attention을 최초로 제안한 위 NMT 모델에서 \(y\)는 디코더가 생성한 번역 결과, \(x\)는 입력 문장이며 양방향bidirectional RNN이다. 중요한 점은 출력 단어 \(y_t\)가 마지막 상태 뿐만 아니라 입력 상태의 모든 조합을 참조하고 있다는 점이며, 여기서 \(\alpha\)는 각 출력이 어떤 입력 상태를 더 많이 참조하는지에 대한 가중치로, \(\alpha\)의 합은 1로 normalized 된. 즉, softmax 값을 사용한다.
\[\alpha _{ ij }=\frac { exp\left( { e }_{ ij } \right) }{ \sum _{ k=1 }^{ { T }_{ x } }{ exp\left( { e }_{ ik } \right) } }\]위 수식에서 \(T_x\)는 디코더 입력 단어의 수 이며, \(e_{ij}\)는 이전 스텝의 히든 스테이트 벡터 \(s_{i-1}\)와 인코더의 \(j\)번째 벡터 \(h_j\)가 얼마나 유사한지를 나타내는 스코어(스칼라)다.5
\[{ e }_{ ij }=a\left( { s }_{ i-1 },{ h }_{ j } \right)\]Attention LSTM
Keras Attention Mechanism을 이용해 LSTM 레이어에 어텐션 벡터를 추가한 모델을 직접 구현해보도록 한다.
a = Permute((2, 1))(lstm_out)
a = Reshape((int(lstm_out_dim), TIME_STEPS))(a)
a = Dense(TIME_STEPS, activation='softmax')(a)
a_probs = Permute((2, 1), name='attention_vec')(a)
attention_mul = merge([lstm_out, a_probs], name='attention_mul', mode='mul')
모델 전체를 도식화하면 아래와 같다. LSTM은 return_sequences=True이며, Permute 레이어는 transpose와 유사한 역할을 한다. 어텐션 벡터에 softmax를 적용해 다시 Permute 했다. Merge는 입력값과의 element-wise multiplication이다.

임의로 입력값에서 15번을 정답과 동일하게 생성하였으며, 그 결과 어텐션 메커니즘은 15번에 가중치를 높게 주는 모습을 확인할 수 있다.

Visualize
이제 How to Visualize Your Recurrent Neural Network with Attention in Keras를 이용해 시각화에 좀 더 집중해보도록 한다. “November 5, 2016”, “5th November 2016”와 같은 human-readable dates를 2016–11–05와 같은 스탠다드 포맷으로 변환하는 어텐션 RNN 모델을 만들어 학습했고, 결과를 시각화 해보도록 한다.
디코더 네트워크
먼저, 디코더 네트워크는 아래와 같다.

어텐션 메커니즘이 컨텍스트 벡터 생성에 참여하며, 디코더 네트워크는 컨텍스트 벡터와 함께 이전 예측을 참조하여 다음 벡터를 생성한다. 빨간색 화살표는 어텐션 메커니즘이 출력 문자 “1”, “6”을 생성하는데 중요한 역할을 한 입력에 가중치를 주는 모습을 도식화 했다.
디코더 레이어
디코더는 백엔드 함수를 호출해 별도의 레이어를 직접 구현했으며, 그 중 가장 중요한 step 함수는 아래와 같은 형태로 입력 시퀀스에 적용된다.
def step(self, x, states):
# obtain elements of the previous time step.
ytm, stm = states
# repeat the hidden state to the length of the sequence
_stm = K.repeat(stm, self.timesteps)
# now multiplty the weight matrix with the repeated hidden state
_Wxstm = K.dot(_stm, self.W_a)
# calculate the attention probabilities
# this relates how much other timesteps contributed to this one.
et = K.dot(activations.tanh(_Wxstm + self._uxpb),
K.expand_dims(self.V_a))
at = K.exp(et)
at_sum = K.sum(at, axis=1)
at_sum_repeated = K.repeat(at_sum, self.timesteps)
at /= at_sum_repeated # vector of size (batchsize, timesteps, 1)
# calculate the context vector
context = K.squeeze(K.batch_dot(at, self.x_seq, axes=1), axis=1)
# ~~~> calculate new hidden state
# first calculate the "r" gate:
rt = activations.sigmoid(
K.dot(ytm, self.W_r)
+ K.dot(stm, self.U_r)
+ K.dot(context, self.C_r)
+ self.b_r)
# now calculate the "z" gate
zt = activations.sigmoid(
K.dot(ytm, self.W_z)
+ K.dot(stm, self.U_z)
+ K.dot(context, self.C_z)
+ self.b_z)
# calculate the proposal hidden state:
s_tp = activations.tanh(
K.dot(ytm, self.W_p)
+ K.dot((rt * stm), self.U_p)
+ K.dot(context, self.C_p)
+ self.b_p)
# new hidden state:
st = (1 - zt) * stm + zt * s_tp
# the probability of having each character.
yt = activations.softmax(
K.dot(ytm, self.W_o)
+ K.dot(stm, self.U_o)
+ K.dot(context, self.C_o)
+ self.b_o)
# a switch so that we can return the
# attention for visualizations
if self.return_probabilities:
return at, [yt, st]
else:
return yt, [yt, st]
return_probabilities=True일때는 어텐션 메커니즘의 결과 까지만 리턴하며, 최종 결과는 LSTM과 유사한 계산 결과를 리턴한다. 여기서는 LSTM을 직접 구현하였는데, 형태는 유사하지만 입력값으로 \(y_{t-1}\), \(s_{t-1}\), \(c_t\)를 받는다는 차이가 있다.
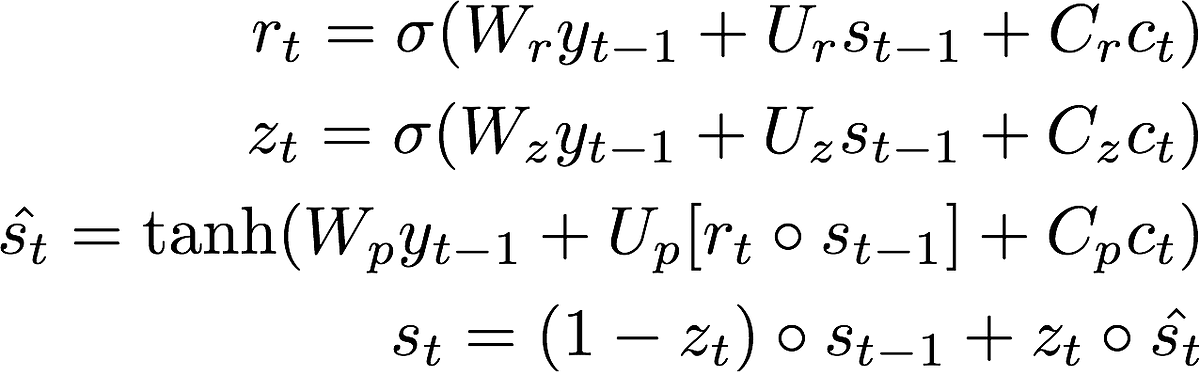
시각화
GPU를 이용해 학습했고, 100번의 epochs로 loss를 0.01 이내로 떨어트렸다. 아래 명령으로 “Saturday Jun 8, 2019”를 시각화 해본다.
python3 visualize.py -e 'Saturday Jun 8, 2019'
결과는 아래와 같다.

2019를 예측하기 위해 “1”, “9”는 입력의 마지막에 영향을 받으며, “0”, “6”은 Jun의 끝 부분에 영향을 받는다. “0”, “8” 또한 day를 의미하는 “8,”에 영향 받고 있다. 그러나 요일 정보인 “Saturday”는 출력에 거의 영향을 끼치지 못함을 확인할 수 있다.
Addition Task 적용
이번에는 이전 글에서 실험한 Addition Task에 Attention을 적용해보고 결과를 비교해보도록 한다. 이번에는 직접 구현하기 보다는 Keras 모델로 미리 만들어둔 라이브러리를 사용 해보도록 한다.
pip install git+https://github.com/farizrahman4u/seq2seq.git
지난 번 Seq2Seq를 구현할때는 시퀀스 단위의 states를 따로 활용하지 않았지만(아래 라이브러리에서 SimpleSeq2Seq 구현) 여기서는 논문6대로 각 시퀀스의 states를 활용하며(라이브러리에서 Seq2Seq 구현) 이를 구현하기 위해 RecurrentShop 이라는 프레임워크를 별도로 사용한다. 현재 이 프레임워크는 Seq2Seq 구현에서 오류가 발생하므로 이를 패치한 아래 버전을 설치한다.
git clone https://github.com/kklemon/recurrentshop
cd recurrentshop
python3 setup.py install
학습 성능
10 epochs 이후 간단히 학습 성능을 비교한 결과는 아래와 같다.
| 모델 | acc, val_acc |
|---|---|
| SimpleSeq2Seq(기존 직접 구현과 동일) | 0.6556, 0.6724 |
| Seq2Seq(논문6 구현) | 0.7643, 0.7604 |
| AttentionSeq2Seq | 0.7430, 0.7297 |
Addition Task는 시퀀스가 길지 않은 모델이며, 이 때문인지 Attention 보다는 Seq2Seq를 논문대로 구현했을때 좀 더 좋은 학습 성능을 보인다.
정리
Attention은 매우 좋은 성능을 보여주며, 특히 쉽게 시각화가 가능하다는 장점이 있다. 이 때문에 최근의 딥러닝 NLP 연구는 주로 Attention을 중심으로 이뤄지고 있으며 Scaled Dot-Product Attention, Self Attention, Multi-Headed Attention, Multi-Dimensional Attention, Re-Attention등 다양한 변형variants이 등장하고 있는 상황이다. 작년에는 CNN도 RNN도 사용하지 않은, Attention 만으로 NMT를 구현한 Transformer 모델이 등장해 주목을 받았으며, 근래 NMT의 대부분은 Transformer 모델로 구현되어 있다.
코드
이 문서에서 사용한 코드는 아래에서 각각 확인할 수 있다.
