Java의 두 Set 교집합 최적화
2015년 5월 19일 초안 작성
서론
두 문서의 유사도를 계산하는 w-shingling 알고리즘은 A/B 두 문서의 슁글(shingle) 사이즈를 아래와 같이 간단한 교집합(intersection)과 합집합(union)으로 유사도를 표현한다.
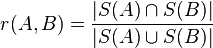
자카드 계수(Jaccard coefficient) 정의와도 동일한데 따라서 교집합(intersection)을 빠르게 계산하는 것이 성능 개선의 핵심이다. 이 부분은 3만회 이상 비교를 진행하는 핫스팟(Hot Spot)이고 약간의 수치 개선 만으로도 전체적인 성능 개선 효과가 크다.
자바에서 두 Set 간 교집합(intersection)을 계산하는 방법은 여러가지가 있으며, 이를 이용해 다양한 교집합을 구해보고 성능을 측정하기로 한다.
성능 측정은 튀는 값을 배제하기 위해 평균(average)이 아닌 중앙값(median)을 취하기로 한다. 중앙값 메소드는 SO에 있는 코드를 참조하여 아래와 같이 작성했다.
private static double median(long[] arr) {
Arrays.sort(arr);
double median;
if (arr.length % 2 == 0)
median = ((double) arr[arr.length / 2] +
(double) arr[arr.length / 2 - 1]
) / 2;
else
median = (double) arr[arr.length / 2];
return median;
}시간 계산은 아래 형태로 100회씩 진행하여 중앙값을 구했다.
for (int i = 0;i<100;i++) {
long startTimeMillis = System.currentTimeMillis();
// do stuff
...
long lastTime = System.currentTimeMillis();
elapsed[i] = lastTime - startTimeMillis;
}
System.out.println("median(elapsed) = " + median(elapsed));실험 및 평가
Straight up Java(JDK)
기존 JDK 기본 라이브러리를 사용한 코드는 아래와 같다.
// JDK 기본 라이브러리
Set<Integer> intersection = new HashSet<Integer>(preSet);
intersection.retainAll(curSet);
intersectionSize = intersection.size();retainAll() 메소드는 java.util.Collection에서 제공하는 JDK 기본 메소드이며 일치하는 Set을 남겨주는 역할을 한다. 즉, 교집합에 해당하는 만큼을 남기며 원본을 조작하므로 원본을 손실하지 않기 위해선 위와 같이 별도의 HashSet을 생성해 담아야 한다.
기존에는 이 기본 메소드를 사용했으며 100회 계산시 109ms 응답 속도 중앙값을 얻었다.
Guava
// Guava
Set<Integer> intersection = Sets.intersection(curSet, preSet);
intersectionSize = intersection.size();Guava에는 Sets.intersection 이라는 좋은 교집합 메소드를 제공하며 크기가 작은 Sets가 앞에 있을 경우 성능이 더 좋다.
Note: The returned view performs slightly better when set1 is the smaller of the two sets. If you have reason to believe one of your sets will generally be smaller than the other, pass it first.
마찬가지로 100회 계산 중앙값은 58ms. 일반적으로 Guava 가 제공하는 기능들은 성능에 있어서 만큼은 좋은 결과를 보여주고 있으며 실제로 이 또한 기존 대비 1.8배 이상 성능 개선 효과가 있다.
No intermediate HashSet(NIH)
기존 보다 응답속도가 훨씬 빨라졌지만 더 성능을 낼 수 있는 방법이 없을까 고민하던차, SO에서 좋은 질문을 발견했다.
Efficiently compute Intersection of two Sets in Java?
게다가 본인이 친절히 성능 테스트를 진행하고 아래와 같이 결과를 제시했다.
Running tests for 1x1
IntersectTest$PostMethod@6cc2060e took 13.9808544 count=1000000
IntersectTest$MyMethod1@7d38847d took 2.9893732 count=1000000
IntersectTest$MyMethod2@9826ac5 took 7.775945 count=1000000
Running tests for 1x10
IntersectTest$PostMethod@67fc9fee took 12.4647712 count=734000
IntersectTest$MyMethod1@7a67f797 took 3.1567252 count=734000
IntersectTest$MyMethod2@3fb01949 took 6.483941 count=734000
Running tests for 1x100
IntersectTest$PostMethod@16675039 took 11.3069326 count=706000
IntersectTest$MyMethod1@58c3d9ac took 2.3482693 count=706000
IntersectTest$MyMethod2@2207d8bb took 4.8687103 count=706000
Running tests for 1x1000
IntersectTest$PostMethod@33d626a4 took 10.28656 count=729000
IntersectTest$MyMethod1@3082f392 took 2.3478658 count=729000
IntersectTest$MyMethod2@65450f1f took 4.109205 count=729000
...PostMethod: 기존 JDK에서 제공하는retainAll()메소드MyMethod1: No intermediate HashSet(이하 NIH) 방식MyMethod2: With intermediate HashSet(이하 WIH) 방식
결과를 살펴보면 어떠한 경우에도 retainAll() 이 가장 느리고 NIH 방식이 WIH 에 비해 두 배 정도 빠름을 확인할 수 있다. WIH 가 정확히 중간(intermediate) 단계가 추가된 만큼 더 느리다.
이에 따르면 성능 개선의 핵심은 중간 단계 배제(No intermediate)였다. 즉, 교집합을 보관할 별도의 Set 을 만들지 않고 단순히 비교해서 수치만 뽑아낼 경우 retainAll() 보다 3배 이상, 중간 단계를 만들때보다도 2배 이상 빠른 응답 속도를 보여준다. 앞서 언급했듯 단순 비교일때는 무시할만한 수치일 수 있으나 현재 이 부분은 3만회 이상 비교를 진행하는 핫스팟(Hot Spot)이고 약간의 수치 개선만으로 전체적인 성능 개선 효과가 크다.
더욱이 w-shingling 알고리즘은 교집합의 수 만 중요하지 교집합의 원소가 무엇인지는 필요하지 않기 때문에 중간 단계 없이 교집합의 수 만 int 로 구해도 충분하다.
MyMethod1의 코드는 아래와 같다.
// No intermediate HashSet
public static int MyMethod1(Set<Integer> set1, Set<Integer> set2) {
Set<Integer> a;
Set<Integer> b;
if (set1.size() <= set2.size()) {
a = set1;
b = set2;
} else {
a = set2;
b = set1;
}
int count = 0;
for (Integer e : a) {
if (b.contains(e)) {
count++;
}
}
return count;
}마찬가지로 100회 계산했고 32ms에 불과하다. 가장 빠르다.
또한 Guava 와 마찬가지로 크기가 작은 Set 가 앞에 왔을때 성능이 더 좋다. 크기 비교를 하지 않고 단순 대입으로 진행한 경우 조금 더 느린 41ms가 나왔다. size()를 여러번 호출해도 성능에 별 영향을 끼치지 않으므로 반드시 크기 비교를 통해 작은 Set 을 앞에 두도록 한다.
결론
교집합을 구하는 방식을 기존 JDK 방식에서 NIH 방식으로 바꿔 기존 대비 3.4배 성능 개선 효과를 얻었다.
| 방식 | 문서 수 / 비교횟수 | 응답 속도 |
|---|---|---|
| JDK | 250 / 31,125 | 109ms |
| Guava | 250 / 31,125 | 58ms |
| NIH | 250 / 31,125 | 32ms |
