수학

• 대수학
  • 점곱dot product, 내적
    • 대수적 정의Algebraic definition
    • 기하학적 정의Geometric definition
  • 로그
  • 점화식
• 정수론
• 해석학
  • 미적분Calculus
• 기하학
• 기타
  • 수학 기호
  • 변수, 상수, 계수
  • Map of Mathematics
  • 확률과 통계
    • 확률의 논리곱, 논리합
  • 수학을 왜 배워야 하는가?

대수학

• 선형대수학
  선형대수학은 방정식, 정확히는 연립일차방정식 ^{system of linear equations}을 푸는 방법과 그에 관련된 이론을 연구하는 학문이다. 선형은 일차식을 뜻하며, 대수는 기호를 조작하여 답을 구하는 방법을 뜻한다. 그러나 현대적 의미의 선형대수학은 크게 세 가지 이론이 융합되어 있다고 할 수 있다. 첫째, 선형대수학의 역사적 근원이기도 한 연립일차방정식의 해법. 둘째, 행렬의 조작. 셋째, 추상적인 벡터공간의 이론이다. (8일간의 선형대수학, 2014)
• 현대대수학(추상대수학 ^abstract) 군론, 환론 group, ring
• 불 대수

대수학은 수학 기호와 이 기호를 조작하기 위한 규칙을 연구한다. (Wikipedia)

• 대수
  • 절댓값^{absolute value}, 항, 집합, 분수^fraction, 비례법
  • 실수^{real number}, 일차방정식^{linear equation}, 부등식^inequality, 퍼센트, 소수^{prime number}
  • 역함수^{inverse function}, 연립일차방정식^{system of linear equations}, 제곱근^{square root}, 이차방정식^{quadratic equation}
  • 이차함수^{quadratic function}, 무리방정식^{irrational equation}, 로그, 지수, 복소수^{complex number}
• 선형대수학
  • 벡터, 일차결합^{linear combination}, 벡터의 내적^{inner product}, 벡터공간
  • 일차변환, 행렬

(누구나 수학, 2018)

점곱^{dot product}, 내적

often called inner product (or rarely projection product), scalar product^스칼라곱

If they’re very similar, the dot product will be large. If they’re very different, the dot product will be small or negative.

대수적 정의^{Algebraic definition}

두 벡터간 내적은 아래와 같이 정의된다.

\(a_x=-3.4, a_y=7.3, b_x=7.1, b_y=7.1\)인 경우
\(a\cdot{b}=(a_x\times{b_x})+(a_y\times{b_y})=27.71\)

기하학적 정의^{Geometric definition}

두 벡터가 반대 방향(180도)이면 내적은 최솟값(\(cos(180)=-1\))이고, 같은 방향(\(cos(0)=1\))일때 최댓값이다.

\(a=8, b=10, \theta=70\)인 경우
\(a\cdot{b}=|a|\times{|b|}\times{cos(\theta)}=27.36\)

로그

\(y = e^x\) ¹

x = 0 일때 기울기가 45도

점화식

점화식^{Recurrence relation}은 n번째의 항을 이전에 나온 항들로 나타내는 공식으로 나타나고, 이 점화식을 만족하는 수열 ^Sequence은 초기값에 따라 유일하게 결정된다. 이렇게 수열을 정의하는 것을 수열의 귀납적 정의(recursive definition)라 한다. (나무위키)
컴퓨터 과학에서 재귀 ^Recursion로 표현한다.

정수론

• gcd: 최대공약수²
• lcm: 최소공배수

해석학

해석학은 대수학과 기하학에 대하여, 미분과 적분을 기초로 함수의 연속성에 관한 성질을 연구하는 수학의 분야이다.

• 수열^sequence, 무한급수^{infinite series}, 도함수^derivative, 적분^integral

(누구나 수학, 2018)

미적분^Calculus

• derivative 도함수
  • 도함수란 각 점에 대해 그 점에서의 미분계수^{differential coefficient}를 대응시키는 함수를 말하고, 미분계수는 그 점에서의 기울기, 즉 순간변화율이다.

미분하면 도함수가 나온다. Sympy 계산 참고

• 미분 differential calculus + 적분 integral calculus = 미적분 calculus
• integral은 summation과 매우 유사하다. 차이점은 sum이 유한 갯수의 합이라면, integral은 무한 갯수의 합이다. (미적분학 갤러리, 2011)

미적분에서 체인룰(연쇄 법칙)은 둘 이상의 합성 함수(composite functions)의 미분을 계산하는 수식이다.

기하학

• 유클리드의 정리
• 사각형, 원, 다각형, 각, sin-cos-tan
• 원기둥, 구, 각기둥, 직육면체

(누구나 수학, 2018)

기타

수학 기호

등호^{equals sign}는 로버트 레코드^{Recorde, Robert}가 1557년에 처음 선보였다. 그 기호를 쓴 것은 “세상에서 그 두 선만큼 똑같은 것은 없기”때문이었다. 이후 등호는 450년이 넘도록 사용되고 있다. (세계를 바꾼 17가지 방정식, 2011) The original form of the symbol was much wider than the present form. In his book Recorde explains his design of the “Gemowe lines” (라틴어로 ‘쌍둥이 선’의 뜻).

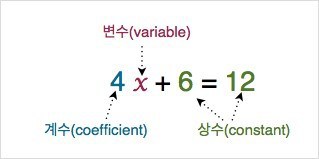
변수, 상수, 계수

³

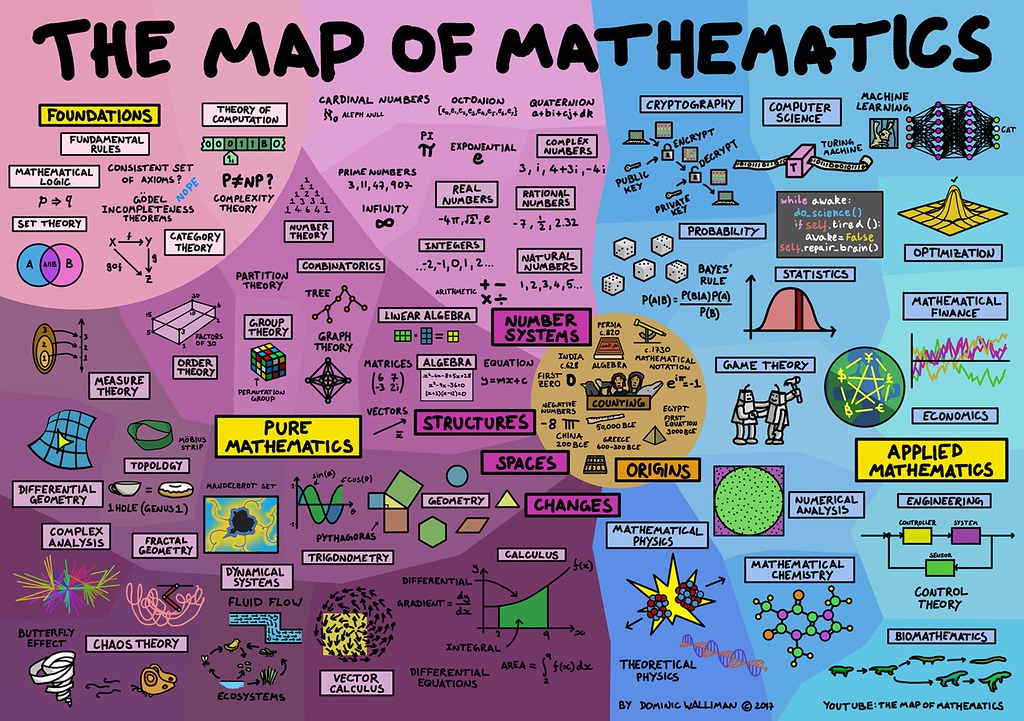
Map of Mathematics

⁴

확률과 통계

• 확률, 베이즈의 정리, 베르누이 시행
• 큰 수의 법칙, 순열^permutation과 조합^combination, 통계학
• 기술통계학, 회귀분석과 상관관계

(누구나 수학, 2018)

확률의 논리곱, 논리합

• 논리곱^{logical conjunction}
  \(P(A\cap{B})=P(A|B)P(B)\) 그렇다면, \(P(A|B)P(A)\)도 마찬가지로 성립하는거 아닌지?

• 논리합^{logical disjunction}
  \(P(A\cup{B})=P(A)+P(B)-P(A\cap{B})\)

수학을 왜 배워야 하는가?

교육이란 학교에서 배운 모든 것을 다 잊어버린 후에, 자신의 내면에 남는 것을 말한다. 그리고 그 힘을 사회가 직면하는 모든 문제를 해결하는 데 사용하기 위해 스스로 생각하고 행동할 수 있는 인간을 만드는 것이다.

아인슈타인 (수학력, 2014)

Last Modified: 2023/12/13 14:40:06