통계학

• 통계학의 종류
• 통계 용어
  • 가설 검정^{hypothesis test}
    • 가설검정 이용하기^{Using Hypothesis Tests}
  • 중심 극한 정리^{central limit theorem}
  • 상관 분석
  • 거짓 상관
    • 잠재 변수^{latent variables}를 간파할 수 있는가?
  • 부트스트래핑^{Bootstrapping}
  • 편찻값
  • 회귀^regression
  • 편향^bias
  • 실험 계획법
  • 기타
• 분포
• 평균의 종류
  • 조화 평균
• 링크

통계학의 종류

• 추측(추리) 통계학 ^{inferential statistics}은 추계학^stochastic으로 불리며, 빈도론적 통계학과 베이즈 통계학이 있다.
• 기술 통계학 ^{descriptive statistics}

통계 용어

• 표준 편차^{standard deviation, stddev, SD}: 분산의 제곱근
  \(\sigma=\sqrt{\frac{\sum\left(x_{i}-\mu\right)^{2}}{N}}\)
  • \(\sigma\) = population standard deviation 모집단의 표준편차
  • N = the size of the population 모집단의 크기
  • \(x_i\) = each value from the population 모집단 각각의 값
  • \(\mu\) = the population mean 모집단의 평균
• 표준 점수^{standard score}는 표준 편차의 배수로 z-score(\(\sigma\))로 부른다.
• 표준 오차^{standard error, stderr, SE}에 대한 설명
  • 평균의 표준오차^{standard error of the mean} = 표준 편차/sqrt{표본 크기}, 아래는 표본수에 따른 표준오차의 변화를 나타냈다.
    
• 비율의 표준오차

‘p-value가 5%를 밑도는가 하는 유의수준으로 가설검정^{hypothesis test}하여 출세율이 16.3%라는 가설 ~ 출세율이 25.7%라는 가설은 부정할 수 없다’라고 말할 수 있다. 이 비율과 평균값+-2SE라는 가장 자주 사용되는 신뢰구간은 5%의 유의수준이고 부정할 수 없는 가설 범위라는 의미로 특별히 95% 신뢰구간이라고 부른다. (통계의 힘 2, 2014)

• 신뢰구간^{confidence interval}=표본평균+-신뢰도상수*표준오차
• 대립가설^{alternative hypothesis}은 우리가 증명하고자 하는 명제
• 귀무가설^{null hypothesis}은 우리가 부정하려는 명제. 귀무 가설은 ‘우연으로 인한 데이터’로 결과는 우연 때문이라 가정한다.
  • 귀무가설 ^{null hypothesis}이 성립한다는 가정 아래 데이터가 얻어지는 확률을 p-value라고 한다.
    • ‘까마귀가 검은지 하얀지가 반반인 경우(귀무가설) 100번 연속으로 검은 까마귀가 발견되었다’는 관찰 결과가 얻어지는 확률의 1조분의 1보다 작다는 것이 p-value이다. (통계의 힘 2, 2014)
  • 어느 정도 p-value가 작아야 ‘존재할 수 없다’고 생각하는지의 기준은 5%를 경계선으로 하는데, 위대한 통계학자 피셔가 일찍이 ‘p-value를 5%로 판단하는 것이 편리하다’는 글을 남긴 것이 계기다. (통계의 힘, 2013) p-value가 5% 이하 일때 null hypothesis를 기각하고 significance ^유의하다고 판단한다.
• 제1종(\(\alpha\)) 오류^{type I error} 아무 차이가 없는데도 차이가 있는 것으로 인식시키는 실수(귀무가설을 잘못 기각하는 오류)
  • 제1종 오류 허용 수준을 가리켜 유의수준^{level of significance}이라 부른다.
• 제2종(\(\beta\)) 오류^{type II error} 본래 차이가 존재하는데도 그것을 못 보고 놓쳐버리는 실수(귀무가설을 잘못 채택하는 오류)
• 통계적 추론^{statistical inference}은 데이터 분석을 통해 기본 확률 분포의 특성을 추론하는 프로세스다.

『통계의 힘』 저자는 임의화 비교실험^{randomized experiment}을 유난히 강조한다. lady tasting tea는 피셔가 진행한 세계 최초로 이루어진 임의화 비교실험이었다. 그러나 ‘현실, 윤리, 감정’의 한계가 있다.

가설 검정^{hypothesis test}

• Student’s t-test^{t 검정} 수십 건 정도의 작은 데이터로도 정확하게 z 검정을 할 수 있으며, 수백에서 수천 건의 데이터가 있을 경우 t 검정과 z 검정의 결과는 일치한다.
• Fisher’s exact test^{피셔의 정확 검정} ‘조합의 수’를 사용하여 수십 건 정도의 데이터로도 정확하게 비율의 차이에 의미가 있는지를 알기 위해 p-value를 구한다.
• Chi-squared test^{카이제곱검정} 구글의 세르게이 브린은 ‘장바구니 분석보다 통계학적 상관분석이 낫다’는 내용의 논문을 발표한 바 있다. 장바구니 분석에서는 개선도나 지지도를 보면서 이것저것 검토해야 하지만, 카이제곱값을 사용했다면 오차에 휘둘리지 않고 관련성이 강한 상품 조합을 자동적으로 찾을 수 있다. 아마존에서도 상품 추천에 이러한 상관분석을 이용한다. (통계의 힘, 2013) 정규 분포를 따르는 여러 데이터를 한꺼번에 취급할 수 있어, 분산분석에 이용할 수 있다. (통계학 도감, 2017)

가설검정 이용하기^{Using Hypothesis Tests}

1. 검정할 가설을 결정합니다. Decide on the hypothesis
   null hypothesis를 사실이라고 가정하고 반하는 증거가 발견될 경우 기각하고 alternative hypothesis(H_1:p < 0.9, 책 기준)를 채택한다.
2. 검정통계를 선택합니다. Choose your test statistic
3. 기각역을 정합니다. Determine the critical region
   우선 유의수준 ^{significance level}을 정할 필요가 있으며, 일반적으로 피셔의 방식에 따라 5%로 정한다.
4. 검정통계를 위한 p-value를 찾습니다. Find the p-value
5. 표본결과가 기각역 안에 들어오는지 확인합니다. Is the sample result in the critical region?
6. 결정을 내립니다. Make your decision

(Head First Statistics, 2008)

중심 극한 정리^{central limit theorem}

라플라스가 얻어낸 결과인 중심 극한 정리^{central limit theorem}는 확률과 통계 분야에서 중요한 전환점이 되었는데, 관측 오차들을 분석하는 데 수학자들이 가장 좋아하는 분포, 즉 종형 곡선을 사용할 수 있는 이론적 근거를 제공했기 때문이다. (세계를 바꾼 17가지 방정식, 2011)

몇 가지 사건이 서로에게 관계 없이(독립적으로) 일어날 때 사건의 수가 많으면 그들 사건의 합이나 평균의 확률 분포는 정규 분포가 된다(중심 극한 정리). (통계와 확률의 원리, 2017)

표본의 크기가 증가함에 따라 원래 데이터 분포의 모양이 어떠하든 거의 상관없이 표본 평균들의 분포가 정규분포의 형태로 다가가는 경향을 의미한다. (p221. 숫자에 약한 사람들을 위한 통계학 수업, 2019)

상관 분석

(통계와 확률의 원리, 2017)

공분산^covariance은 두 변수가 각각 평균에서 얼마나 멀리 떨어져 있는지를 나타낸다. 성향 점수 매칭법 ^{propensity score matching}으로 다수의 공변량 ^covariate으로 성향 점수를 계산할 수 있다.

상관 계수^{correlation coefficient}는 r로 표기한다. 상관의 정도를 나타내는 지표로 -1에서 1 사이의 값을 가지며, 방향^direction과 강도 두 가지 정보를 제공한다. 0이면 강도가 낮다. 골턴의 제자인 피어슨(1857 ~ 1936)이 계산 방법을 고안했다.

(수학 없이 배우는 데이터 과학과 알고리즘, 2017) (통계학 도감, 2017)

거짓 상관

Spurious relationship 일본에서는 ‘의사 상관’이라고 하는데 ‘거짓 상관’으로 번역하는게 맞을 것 같다. 두 사건이 실제로는 관련이 없는데 우연의 일치, 보이지 않는 제3의 요소의 존재^{the presence of a certain third, unseen factor}로 인과 관계가 있는 것으로 추측되는 것을 말한다. unseen factor는 “common response variable”, confounding factor^{교란 요인} 또는 “lurking variable”로 부르기도 한다. 또는 ‘제3의 변수’. (원인과 결과의, 경제학, 2018)는 제4의 변수, 조작 변수로 언급하기도 했다.

피어슨은 이 현상을 가짜 상관이라 불렀다. (통계학을 떠받치는 일곱기둥 이야기, 2016)

상관계수는 선형적인 상관관계만 측정합니다(x가 증가하면 y는 증가하거나 감소합니다). 그래서 비선형적인 관계는 잡을 수 없습니다. (핸즈온 머신러닝, 2017)

미국 청소년의 탄산음료 소비와 폭력성 간의 상관관계 연구로 한 신문은 이것을 “탄산음료가 10대 청소년을 폭력적으로 만든다”라고 보도했다. 하지만 폭력성이 갈증을 불러일으켰을지 모른다는 주장도 그럴듯하게 들리지 않는가? 또는 둘 다에 중대한 영향을 미치는 공통 요인이 있는지도 모른다. 이처럼 측정되지 않은 잠재적 공통 원인을 잠복 변수 ^{lurking variable}라고 한다. 잠복변수는 전면에 드러나지 않아 조정 대상이 되지 못하므로, 관측 데이터로부터 잘못된 결론을 내리는 실수를 유도한다. (p131. 숫자에 약한 사람들을 위한 통계학 수업, 2019)

잠재 변수^{latent variables}를 간파할 수 있는가?

• 40대에 출산한 여성은 장수하는 경향이 있다. 100세 이상의 여성들과, 73세에 사망한 여성들을 비교하면, 장수하는 여성들에서 고령 출산의 비율이 높았다. (1997년 nature 논문을 바탕으로 작성)
  • 40세에 출산할 수 있을 정도로 건강하며, 그래서 장수할 수 있었다. 잠재 변수: 건강 (통계와 확률의 원리, 2017)

부트스트래핑^{Bootstrapping}

무작위 샘플링을 대체하여 수행되는 테스트 또는 메트릭이다. 부트스트랩은 인위적인 자료 집합을 만들어내는 컴퓨터를 이용해야 하는 몇 가지 방법 중에서 가장 탁월한 것이다. 하버드의 통계학자 퍼시 디아코니스는 에프론 박사의 기술은 “매우 간단하지만 상당히 효과적”이라고 말했다. (뉴욕타임스 수학, 2013, 1988년 기사)

복원 추출을 반복해 추정값의 변동성에 관한 아이디어를 얻는 과정을 데이터의 부트스트랩이라고 한다. (p219. 숫자에 약한 사람들을 위한 통계학 수업, 2019)

편찻값

평균일때 50을 가르키는 일본어 hensachi(편차치)로 일본에서 출판된 통계학 책에만 등장하며 일본에서만 주로 쓰인다. 나무위키에 따르면 수능 학력 편차치로 쓰인다고. 우리나라에서도 표준점수로 비슷하게 쓰인다. 영어로는 deviation value의 의미이고 영어권에서는 사용하지 않는다.

회귀^regression

골턴은 1889년 『자연적 유전』 에서 회귀^regression라는 개념을 논했다. 키가 큰 사람과 키가 작은 사람이 만나 아이를 낳으면 자녀들의 평균 키는 중간값, 즉 부모의 평균 키여야 했다. 이후 세대들이 이어지면서, 분산은 크게 변하지 않고 원상태를 유지하는 한편 평균 키는 고정된 중간값으로 ‘회귀’한다. (세계를 바꾼 17가지 방정식, 2011) ‘평균으로의 회귀’

편향^bias

생존 편향^{Survivorship Bias}

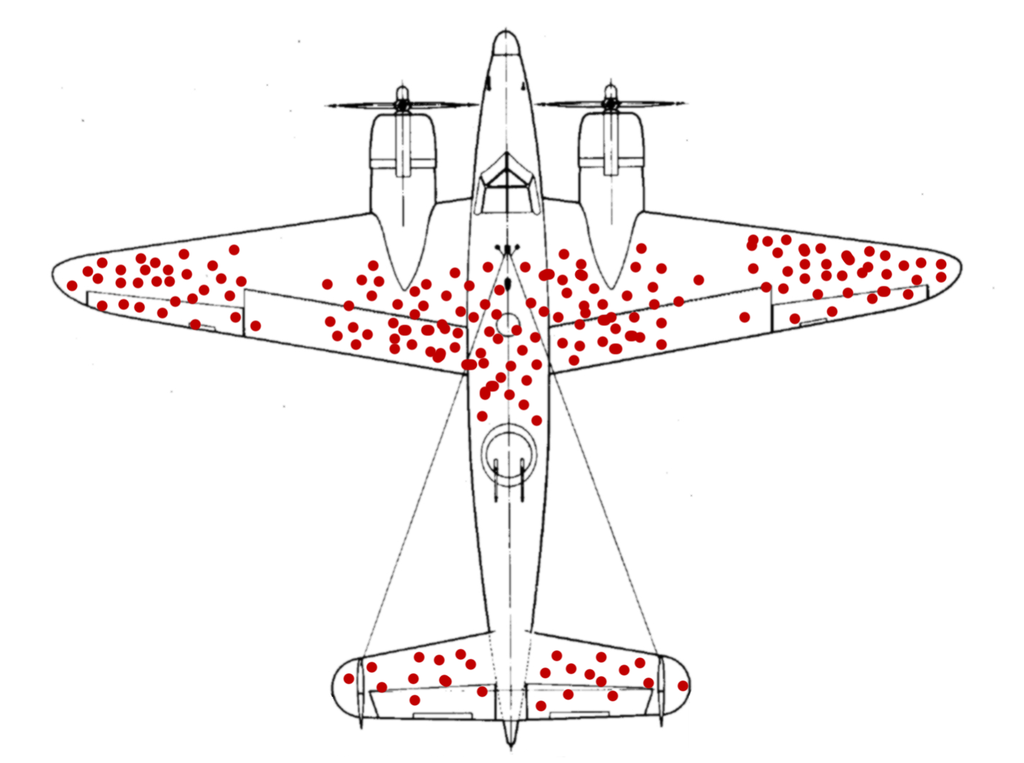
2차 세계대전 당시 통계학자 아브라함 발드가 살아남은 것만 주목하고 실패한 것은 고려하지 않는 ‘생존 편향’의 문제점을 지적했다. (틀리지 않는법, 2015)

Science Isn’t Broken 연구자들은 주장하는 명제에 부합하는 통계를 산출하기 마련이다. 위와 비슷한 이야기. 미려한 이미지가 인상적이다.

연구자들은 환자들이 날씨의 어떤 면을 고려하든지 관절염 환자의 증상과 날씨 사이에서 아무 연관성을 발견하지 못했다. (뉴욕타임스 수학, 2013, 1996년 기사) 농구에서 핫 핸드가 근거 없는 믿음이라는 것과 마찬가지다.

통계학이 재판소에서 이용될때 그 영향이 진실을 호도하기 쉽다. 믈로디노프는 O.J 심슨 재판을 회상한다. 검사는 피고 심슨을 상습적인 아내 학대자로 묘사했다. 하지만 미국에서 해마다 4백만 명의 여성이 남편에게 구타를 당한다. 그 중 남편에게 살해되는 사람은 2,500분의 1에 불과하다. 배심원단은 설득력 있는 변론이라고 보았지만, 겉으로만 그럴싸한 논거다. 니콜 브라운 심슨은 이미 죽었다. 이 사건에 대한 적절한 질문은 살해당한 모든 피해 여성의 몇 퍼센트가 학대자에 의해서 죽느냐는 것이다. 믈로디노프가 주목한건 재판에서 그 답이 나오지 않았다는 점이다. 답은 90%였다. 이런 종류의 수학에서 변호사들은 의사들과 별 다를바 없는 것 같다. 하지만 배심원단의 수준은 더 심각하다. (뉴욕타임스 수학, 2013, 2008년 기사)

실험 계획법

피셔의 3원칙 ^{basic principles of experimental designs}

1. 반복 ^replication
2. 무작위화 ^{randomization}
3. 국소관리 ^{local control}

국소관리란 공간적, 시간적인 실험의 장을 작게 나누고, 그 속에서 실험을 실시하고 분석하는 것을 말한다. (통계학 도감, 2017)

기타

이산형 ^discrete, 연속형 ^continuous에서 이산형은 sum, 연속형은 적분 ^integral이 된다.

인과 관계 ^correlation에 불과한데도 상관 관계 ^causality로 혼동하는 경우가 있다. 둘 사이의 명확한 구분이 필요하다. (원인과 결과의, 경제학, 2018)

‘건강검진을 받았기 때문에 장수할 수 있는 것(인과관계)’이 아니라, ‘건강검진을 받을 정도로 건강에 대한 의식이 높은 사람일수록 장수하는 것(상관관계)’으로 해석하는 것이 타당할 수 있다. (원인과 결과의, 경제학, 2018)

이중차분법 ^{differences in differenses; DID}은 두 집단의 difference를 difference한 두 시기로 비교해보는 것이다. 보통 정책 시행 전후로 수혜 집단과 비수혜 집단의 차이를 비교해보는데 쓰인다. (출처)

카드 카운팅을 발명한 에드워드 소프. 경우의 수 ^{number of cases}에서 카드 카운팅은 계산하기가 조금 복잡한 편이다. (넘버스, 2017)

분포

¹

• 정규 분포
  누적 분포(cdf; cumulative distribution)를 그래프로 그려 실제값(actual ratio)가 얼마나 비슷한지 직접 도식화한게 있다.

2\(\sigma\)면 좌우 4.6%에 속한다.

확률 밀도 함수 ^{pdf; Probability density function} 즉, 적분값이 확률이 된다. 6시그마 활동이란 6\({\sigma}\)구간의 밖. 즉, 100만분의 3.4 수준으로 불량품을 줄이려는 활동을 말하며, 1980년대 후반 미국 모토롤라 연구진이 경영과 품질개선의 일환으로 시작했다. (통계학 도감, 2017)

• 이산 확률 분포^{discrete probability distribution}
  확률 변수가 정해진 값을 갖고 있을때. 주어진 구간에서 어떠한 실수 값이라도 가질 수 있는 경우 continuous probability distribution^{연속 확률 분포}이다.

• 이항 분포^{Binomial distribution}
  성공이나 실패처럼 결과가 두 종류밖에 없는 시행을 처음 이야기한 통계학자의 이름을 따와 베르누이 시행^{Bernoulli trial}이라고 한다.

• 균등 분포 ^{uniform distribution}
  각 사상이 일어나는 확률이 같은 분포

• 기하 분포^{Geometric distribution}
  베르누이 시행에서 처음 성공까지 시도한 횟수 X의 분포 또는 실패한 횟수 Y=X-1의 분포. 대개의 경우 X의 분포를 가리키는 것이 일반적이다.

• 포아송 분포^{Poisson distribution}
  시행 ^trial 횟수가 아주 많고(n이 크다), 사상 ^event 발생의 확률(p)이 아주 작을때의 이항 분포다. 런던 대공습의 폭탄이 정밀 타격인지 분석 결과, 푸아송 분포를 따랐다. (신은 주사위 놀이를 하지 않는다, 2014)

평균의 종류

10, 90이 있을때

• 산술 평균 ^{arithmetic mean}: 50
• 기하 평균 ^{geometric mean}: \(\sqrt{(10\times 90)} = 30\)
• 제곱 평균 ^{root mean square; rms}: \(\sqrt{\frac{10^2+90^2}{2}} = 64.03\)
• 조화 평균 ^{harmonic mean}: \(\frac{2}{\frac{1}{10} + \frac{1}{90}} = 18\)

조화 평균

수학에서 조화 평균 ^{harmonic mean}은 주어진 수들의 역수의 산술 평균의 역수를 말한다. 평균적인 변화율을 구할 때에 주로 사용된다. (위키피디어) 서로 다른 거리를 정규화^normalize하는 효과가 있다.

(통계학 도감, 2017)

링크

통계 링크

Last Modified: 2021/06/08 13:03:45