사다리 게임, 절대 걸리지 않는 법
2018년 1월 15일 초안 작성
본론
실험 증명
확률과 통계 문제 만큼 컴퓨터로 실험하기 좋은, 흥미로운 주제도 흔치 않다. 개인적으로 가장 존경하는 과학자가 실험 과학자로 유명했던 마이클 패러데이 이기도 하고, 아인슈타인도 패러데이를 존경해 침실 벽면에 그의 초상화를 붙여두었다고 한다.
컴퓨터를 통한 최초의 수학 증명은 1976년 4색 정리였다. 당시만 해도 고작 1,936개의 모델을 계산하는데 두 대의 컴퓨터로 50일이 넘게 걸렸다. 뿐만 아니라 수학적으로 우아하지 못하다는 비판이 잇따랐지만 역사적으로 볼때 공학적 기술은 언제나 이론을 앞서갔다.
얼마전에 봤던 해커를 위한 통계학 발표도 인상적이었다. 수학적 통계를 해커들의 컴퓨터 실험으로 증명하는 방식은 매우 인상적이었다. 이 발표를 본 이후 수식을 접하게 되면 항상 실험을 통해 증명하려는 습관이 생길 정도다. 최근에는 수능 수학 문제를 코드로 풀어보는 시도에도 깊은 인상을 받았다. 더 이상 공식을 외워서 푸는 방식이 아닌 코드로 공식을 유도하고 이를 컴퓨터 계산으로 풀이하면, 수학의 원리를 깨닫는 한 편 진정한 수학의 재미를 느낄 수 있다.
여기에 쓰인 도구는 파이썬과 주피터 노트북 그리고 컴퓨터 뿐이다. 컴퓨터만 빼면 모든건 무료로 갖출 수 있다. 여기서도 동일한 도구를 사용해 풀이해 보도록 한다.
한중일 전통 게임
먼저 관련된 통계 자료를 찾아봤다. 사다리 게임이라면 한 번쯤 통계학에서 관심 가질 만한 주제인데 자료가 너무 없다. 왜 이렇게 자료가 부족한가 봤더니 사다리 게임이란 것이 한중일에서만 통용되는 게임이다. 영미권에서는 사다리 게임을 하지 않고, 따라서 영어 통계책에는 사다리 게임이 한 번도 등장하지 않았던 것이다. 그러고 보니 『통계의 힘』 도 일본 책이고, 사다리 게임이라고 간간히 접한 정보들은 전부 한글로 된 정보뿐이었다.
사다리 게임을 게임 구현이 아닌 출발과 결과를 계산할 수 있게 풀이한 오픈소스도 찾을 수가 없었다. 누군가 구현했을거라 생각했는데 한중일에 제한된 게임은, 영어로 된 코드를 찾을 수가 없었다. 생각해보면 이 글 또한 여기서 자세히 구현한다 해도 마찬가지로 한글로 써졌고 영어권에서는 이 글을 찾을 수 없을 것 같다. 아쉬운 부분이다.
구현 실험
결국 사다리 게임을 직접 구현해보기로 했다. 최대한 단순하게 구현하기 위해 각각의 다리와 계단을 모두 2차원 배열에 표현하고 출발지에서 시작해 각 단계별로 계단 유무를 판별하여 이동을 거쳐 최종 도착지의 값을 구하는 방식으로 구현했다.
먼저 『통계의 힘』 책에 나온 결과부터 살펴보자. 8개의 다리가 있고, 12개의 계단이 있다. 4번이 술래일때 1,000번의 반복 시뮬레이션을 통해 아래와 같은 결과를 제시했다.
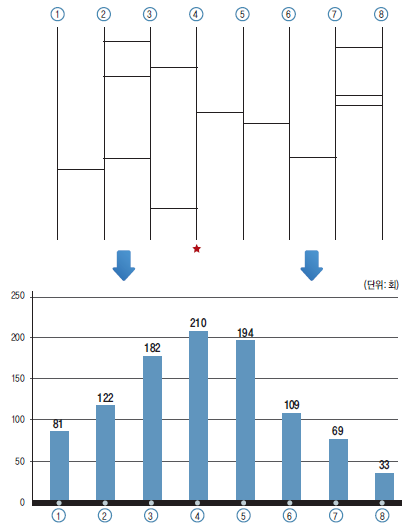
이를 동일하게 실험하여 어떤 결과가 나오는지 살펴봤다.
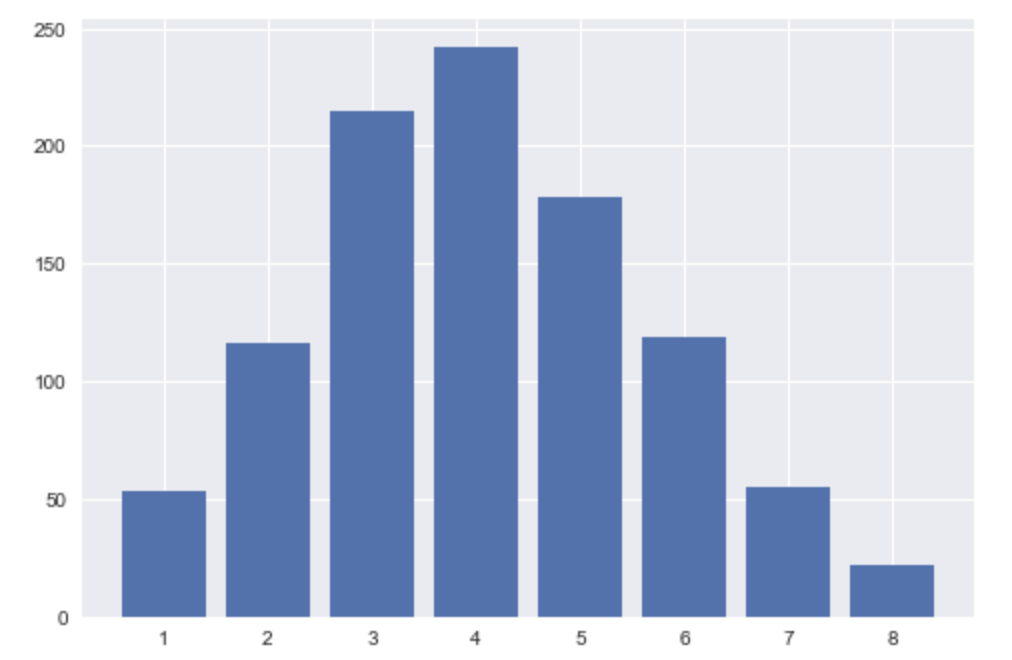
책에서와 비슷한 정규분포가 나온다.
3번과 5번에서 약간 다른 모양이 나왔지만 이는 실험 횟수가 부족해서로 보인다. 큰 수의 법칙Law of large numbers에 따라 실험 횟수가 충분하다면 거의 동일한 형태가 될 것이다.
출발지에 따른 결과 분포
그렇다면 각각의 출발지에 따른 결과 분포는 어떻게 될까. 일반적으로 우리는 사다리 게임이 공평할거라 기대하고 있다. 그래야 이 게임이 수백년 간이나 이어져 내려왔을테니까. 그렇다면, 여기서는 ‘사다리 게임은 공평하지 않다’ 를 귀무가설null hypothesis로 택하고 이를 기각하기 위해 데이터를 다뤄보도록 한다.
같은 조건(8개의 다리, 12개의 계단, 1,000번 반복)으로 출발지에 따른 결과 분포를 실험해본 결과는 아래와 같다.
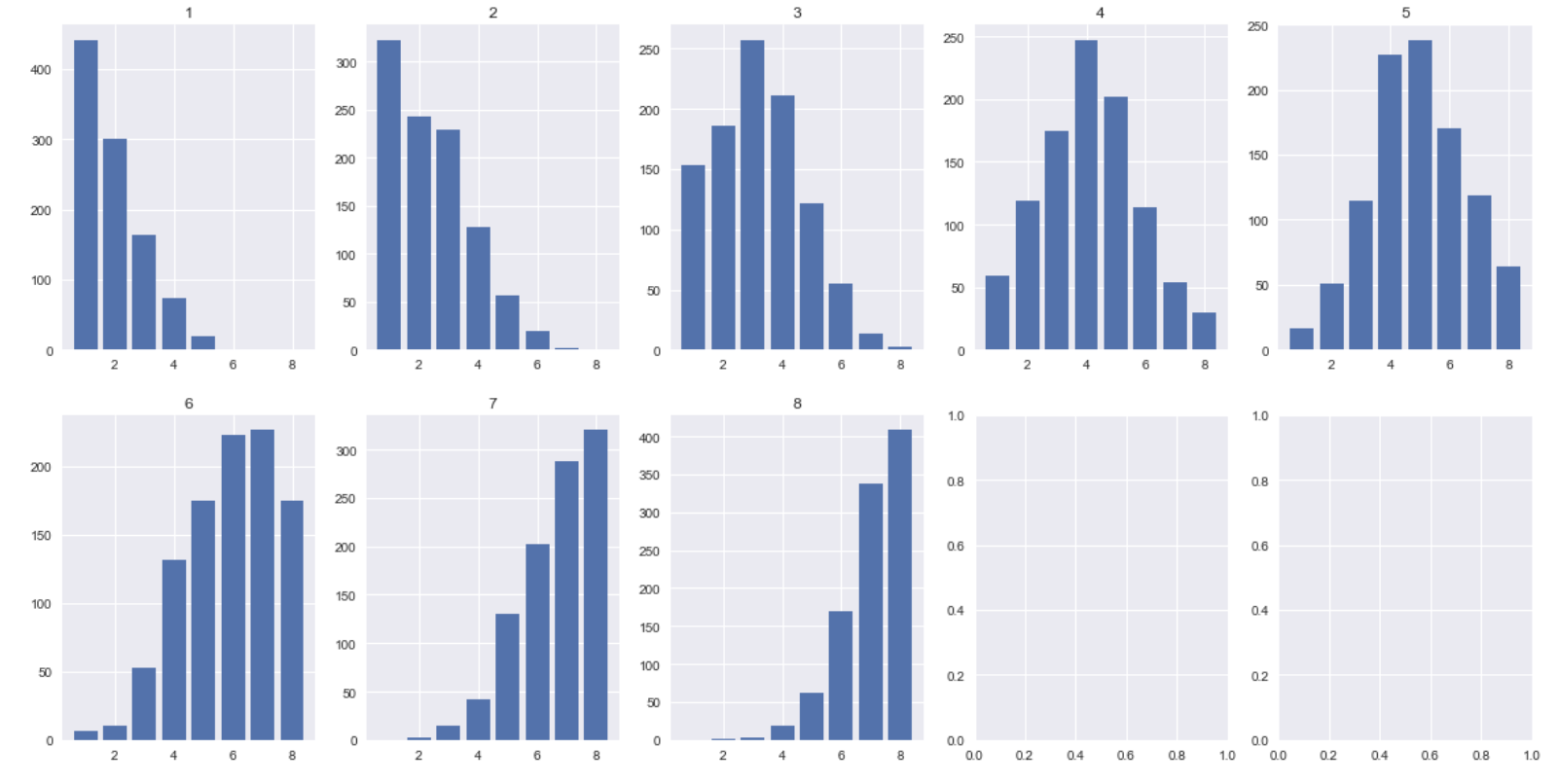
이대로만 보면 전혀 공평하지 않다.
중앙 부근에서 출발하면 항상 정규 분포를 띄며, 심지어 끝에서 끝까지 도달하지도 못한다. 1번에서 출발하면 8번에 도착하지 못하는 것이다. 이 말은 8번이 술래일때 1번을 택하면 절대 걸리지 않는다는 의미이기도 하다. 과연 그럴까. 정말 사다리 게임은 불공평한 게임일까.
계단 수에 따른 결과 분포
여기서 우리는 1번에서 출발하면 8번에 도착할 수 없다는 점에 주목해보도록 한다. 왜 도달하지 못할까. 이렇게 되면 게임 자체가 성립될 수 없는데, 혹시 계단의 갯수가 부족해서는 아닐까. 그렇다면 계단의 갯수를 늘려가며 실험해보도록 한다.
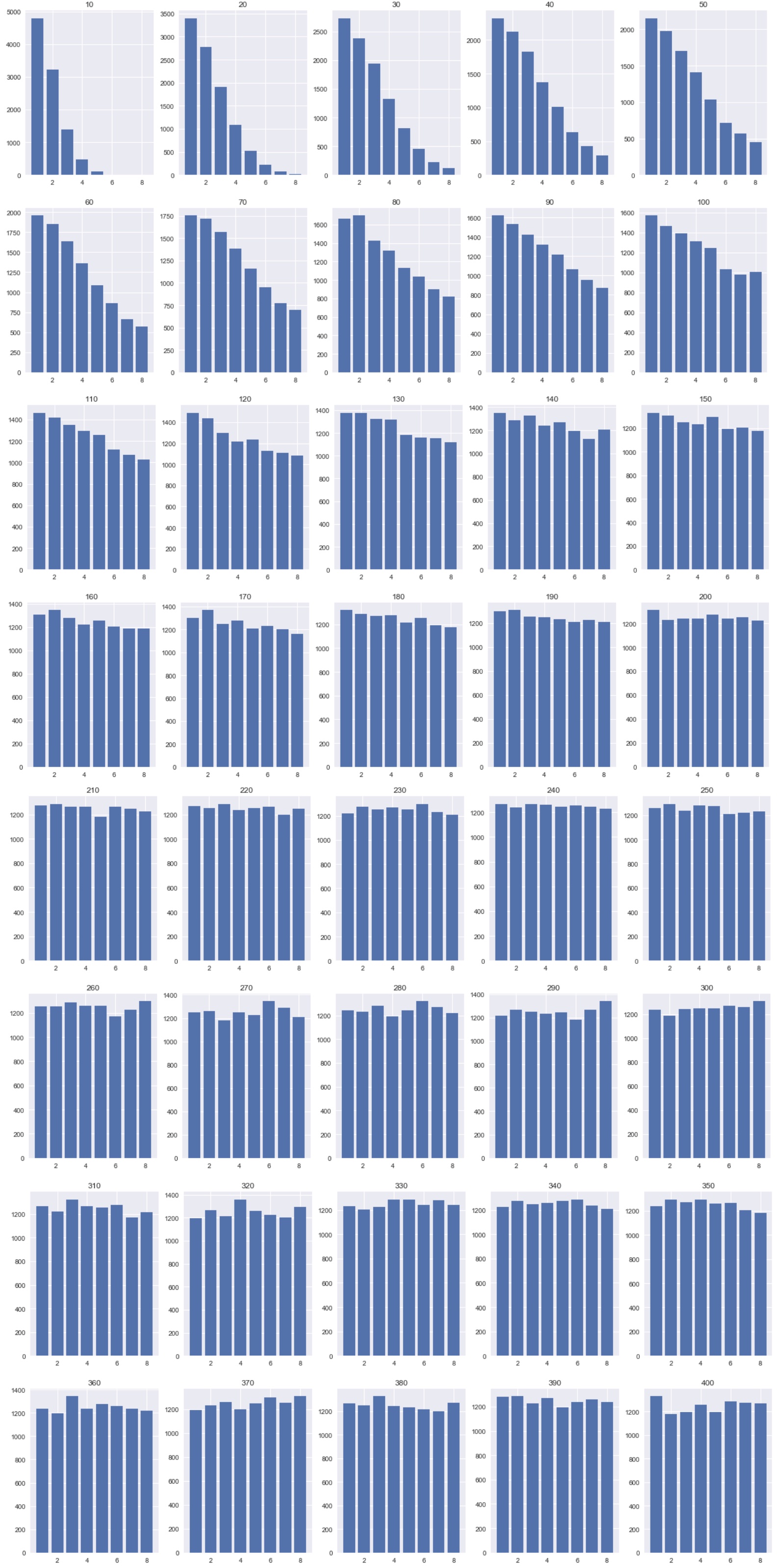
계단의 갯수를 10개부터 차츰 늘려가며 400개까지 만들었을때, 1번에서 출발한 도착점 분포다. 실험은 실제 확률에 근사하도록 각 1만회씩 충분히 시행했다.
계단의 갯수가 적을때는 확연히 치우친 모습을 보인다. 하지만 서서히 균등 분포uniform distribution를 띈다. 유의한significance p-value 기준은 관례상 5%로 하며, 이는 통계학의 아버지 피셔가 일찍이 제안했던 수치를 그대로 답습하도록 한다. 여러번의 실험을 통해 균등 분포가 95% 이상을 보이는 지점은 약 300개 이상일때 임을 찾아냈으며 이를 통해 계단이 300개 이상일때 ‘사다리 게임은 공평하지 않다’는 귀무가설을 기각한다.
수식
일본어 위키피디어에 따르면 참가자가 \(N\)일때 필요한 계단의 갯수를 계산하는 수식은 아래와 같다.
우리가 실험한 값과는 약간 차이가 있는데 이는 상수 계수를 생략한 대략적인 추산이기 때문이며 크게 중요하지 않다. 여기서 중요한 점은 수식이 지수란 점이며, 이는 참가자(다리의 수)가 많을수록 필요한 계단의 수가 기하급수적으로exponential 증가함을 뜻한다.
즉, 위 수식을 계산하면 \(N=8\) 일때 392이며, 9일때는 576, 10일때는 810이 되는데, 이는 참가자가 10명일때 8명에 비해 2배나 많은 계단이 필요하다는 얘기다.
현실
계단의 수가 충분하면 사다리 게임은 공평하다. 적어도 수백년간 우리가 해왔던 게임이 잘못되지 않았다는데 안도한다. 그러나, 현실적으로 8명이 참여하는 게임에 계단을 300개나 그릴 순 없다. 참가자가 늘수록 이 값은 무한히 증가한다. 여러 사람이 모여 연습장에 빠르게 그려 하는 사다리 게임의 특성상 『통계의 힘』 책에서 조언한 것 처럼 확률적으로 낮은 곳을 택하는 것이 유리하다.
12개일때 결과 분포
그렇다면 다시, 계단 수가 12개일때 결과 분포가 어떤 형태를 이루는지 살펴보자.
대부분의 사다리 게임에선 이처럼 계단 수가 부족할 것이고 이 경우 확률이 낮은 쪽을 고르는 것이 유리하다. 어느 쪽이 확률이 낮은지 실험을 통해 살펴보도록 한다.
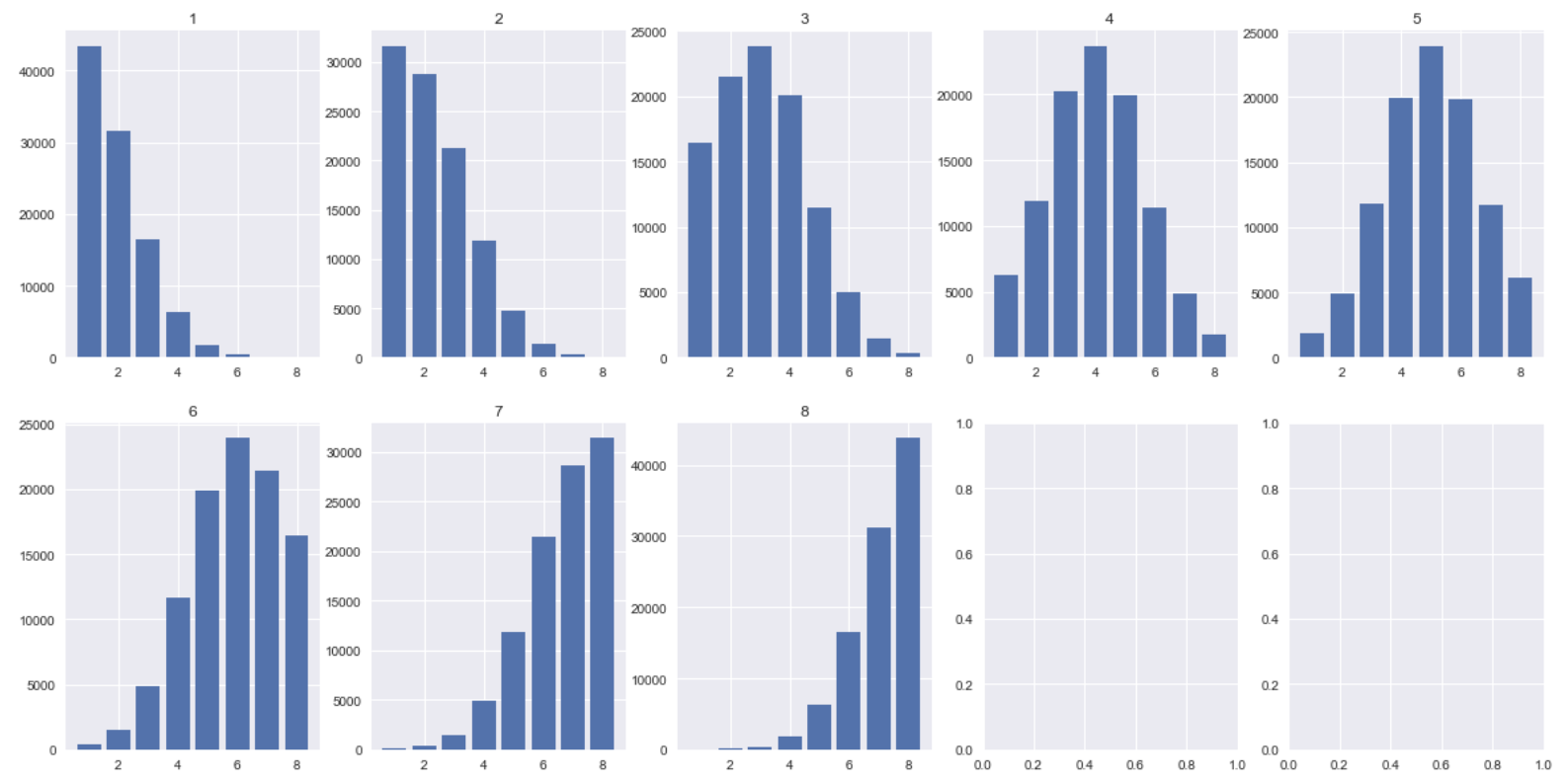
이전보다 훨씬 더 많은, 각각 10만회씩 실험을 통해 실제 확률에 근사하도록 했다. ‘출발지에 따른 결과 분포’ 처럼 결과가 들쑥날쑥하지 않고 고르게 분포한 것을 확인할 수 있다.
마찬가지로 정규 분포를 띄는데 특이한 점이 있다. 2번에서 출발하면 2번에 도착하는 것보다 오히려 1번에 도착할 확률이 더 높다는 점이다. 마찬가지로 7번에서 출발하면 8번에 도착할 확률이 가장 높다. 이런 추세는 3번에도 이어진다. 1,2번에 도착할 확률이 나머지 4,5,6,7,8 모두를 합친 것 보다 더 높다. 6번도 마찬가지다. 치우친 쪽으로 결과 쏠림 현상이 보인다.
이를 통해 도착점이 한 쪽에 치우쳐 있는 경우 가능한 반대쪽을 택해야 걸릴 확률이 낮다는 점을 실험 결과를 통해 확인할 수 있다.
TL;DR
위에 나온 내용을 모두 정리하면 아래와 같다.
- 충분히 많은 계단을 그리면(8명이 참가할 경우 최소한 300개) 도착점은 고르게 분포하지만, 현실적으로 그렇게 많이 그릴 수 없다.
- 따라서, 출발점은 도착점에서 가능한 먼 곳을 택한다.
- 도착점이 한쪽으로 치우쳐skewed 있는 경우 걸릴 확률은 치우쳐 있는 방향이 더 높다. 따라서, 반대 방향을 택해야 한다.
- 도착점이 오른쪽에 치우쳐 있는 경우 출발점은 가능한 왼쪽으로 멀리 택한다.
- 도착점이 왼쪽에 치우쳐 있는 경우 출발점은 가능한 오른쪽으로 멀리 택한다.
정리
이제 여러분은 더 이상 점심을 사지 않아도 된다.
물론 처음 한 두번은 우연히 걸릴지도 모르겠지만 1년 내내 사다리 게임으로 점심을 사기로 정했다면, 그리고 여러분이 여기 나온 내용을 충분히 숙지하고 사다리 게임을 했다면, 큰 수의 법칙에 따라 여러분은 1년 동안 점심을 가장 적게 산 사람으로 기억될 것이다.
통계의 마법이다.


