About Tumblr

NumPy로 구현하는 라마 3 모델

라마 3 모델의 실제 동작 가능한 구현을 통해 정확한 구조를 이해한다.

2024년 5월 14일 작성

For a detailed explanation in English, see Llama 3 implemented in pure NumPy. [English Version]

개요

메타에서 공개한 라마 3 모델이 연일 화제다.

기대했던 대로 압도적인 스케일과 성능을 자랑한다. 2만 4천 장의 GPU, 15T 학습 데이터, 1천만 건의 인스트럭션 데이터, 1.3M GPU hours, 모든 게 압도적이다. 당연히 성능도 좋다. 한 가지 재밌는 사실은 모델 구조는 변하지 않았다는 점이다. 물론 모든 모델이 GQA를 사용하는 구조로 바뀌었지만 이건 지난 라마 2때도 70B에서 이미 적용됐기 때문에 사실상 동일한 모델 구조를 갖고 있다고 할 수 있다.

여기서는 정확한 구현을 위해 실제로 동작이 가능한 형태로 구현해 보겠다. 또한 보다 직관적으로 모델 구조를 이해할 수 있도록 오로지 NumPy만으로 라마 3 모델을 구현한다. 모델은 안드레이 카파시가 llama2.c를 만들며 학습한 stories15M 모델을 사용하며, 이 파일을 컨버터를 이용해 numpy compressed 포맷으로 저장한 다음 활용한다. 실제로 카파시가 라마 2 구조로 학습한 모델을 직접 읽어 들여서 실행 가능한 코드로 구현하겠다. 한 가지 주의할 점은 stories15M 모델은 GQA를 사용하지 않았다는 점이다. 따라서 여기서도 GQA는 코드로 구현만 해놓되 모델 동작을 위해 적용은 하지 않도록 한다.

구조

라마의 모델 구조는 42dot LLM과 완전히 동일하므로 42dot 블로그에 올라온 그림을 가져오면 다음과 같다.

모델의 파라미터는 다음과 같다.

# Model params for ./stories15M.model.npz
dim: int                    = 288       # D
n_layers: int               = 6
n_heads: int                = 6         # QHN, HN, HD = 48
n_kv_heads: Optional[int]   = None      # KVHN = 6
vocab_size: int             = 32000     # VS
max_seq_len: int            = 256       # M
max_new_tokens: int         = 50

주석에 부여한 D, HN, HD, VS, M등의 명칭은 코드 내에서 각 변수의 shape을 관리하기 위한 용도로 쓴다. 아울러 모델 그림의 24x와 달리 해당 모델은 레이어가 6개이므로 6x 반복한다는 점에 유의 바란다.

RoPE #1

가장 먼저 RoPE 임베딩을 위해 cos, sin을 미리 계산하는 과정이 필요하다. 이 값은 이후에 Q, K에서 사용한다. 계산은 모든 요청에 대해 한 번만 하면 되므로 캐싱이 가능하다. 크기는 HD(48)//2이며, base(10000)의 지수배라 큰 값이 될 수 있지만 최댓값이 1을 넘지 않으므로 0 ~ 1 사이의 스케일링된 값, 이후에 다시 \(1 \sim \frac{1}{10000}\)사이의 값으로 변환된다.

                        np.arange(0, 48, 2)  # [24,]
  1.0 / (base(10000) ** ([0, 2,          ..., 44,         46] / 48))
= 1.0 / (base(10000) **  [0, 0.04166667, ..., 0.9166667,  0.958333344])
= 1.0 /                  [1, 1.4677993,  ..., 4641.59,    6812.9194]
=                        [1, 0.68129206, ..., 0.00021544, 0.00014678]

계산 결과는 max_seq_len(256) 만큼 np.outer를 한 다음 cos, sin값을 구한다.

# [256,] x [24,] = [256, 24]
freqs = np.outer([0 ~ 255], [1, 0.68129206, ..., 0.00021544, 0.00014678])
self.freqs_cos: Array["M, HD//2"] = np.cos(freqs)
self.freqs_sin: Array["M, HD//2"] = np.sin(freqs)

cos와 sin의 히트맵은 다음과 같다.

stories15M 모델은 max_seq_len(256)이지만 가로축 24까지 값을 모두 활용하면 8K까지도 확장이 가능할 것 같다.

RMSNorm

RMSNorm은 기존에 미니 배치 또는 레이어 통계를 사용하는 것과 달리 activation 값의 제곱근 평균을 기준으로 정규화한다. 이 방식은 미니 배치의 크기나 레이어에 관계 없이 activation에 일관되게 스케일링 된다는 잇점이 있다. 이외에도 다른 normalization 기법과 마찬가지로 별도의 학습 파라미터를 갖고 있다.

1

수식 구현은 다음과 같다.

z: Array["B, L or 1, 1"] = (x ** 2).mean(-1, keepdims=True) + self.eps
z: Array["B, L or 1, D"] = x / np.sqrt(z)
return z * self.weight

QKV

QKV를 계산하는 방식이 GPT에서는 하나의 Weight에 matmul을 한 다음 split해서 사용했는데, 라마는 QKV의 Weight를 각각 갖고 있어 각자 matmul을 해야한다. 이후에 Multi-Head를 위해 각자 reshape해서 헤드별로 구분한다.

# QKV
xq: Array["B, L or 1, D"] = x @ self.q_weight
xk: Array["B, L or 1, D"] = x @ self.k_weight
xv: Array["B, L or 1, D"] = x @ self.v_weight

# ["B, L or 1, D"] -> ["B, L or 1, QHN or KVHN,  HD"]
xq: Array["B, L or 1, QHN,  HD"] = xq.reshape(B, L, self.n_local_heads, self.head_dim)
xk: Array["B, L or 1, KVHN, HD"] = xk.reshape(B, L, self.n_local_kv_heads, self.head_dim)
xv: Array["B, L or 1, KVHN, HD"] = xv.reshape(B, L, self.n_local_kv_heads, self.head_dim)

RoPE #2

이제 앞서 계산한 값을 이용해 실제로 RoPE를 적용하는 단계다.

2

RoPE는 absolute와 relative의 특징을 모두 지닌 새로운 유형의 position encoding 기법으로 양쪽 모두의 특징을 지녀 성능이 뛰어나다. 이 값은 Q와 K에만 적용하며, 각각의 입력을 홀짝으로 나눈 다음 cos, sin을 곱해서 더하고 뺀 결과를 다시 reshape으로 합쳐서 리턴한다.

xq_out_r: Array["B, L or 1, QHN,  HD//2"] = xq_r * freqs_cos - xq_i * freqs_sin
xq_out_i: Array["B, L or 1, QHN,  HD//2"] = xq_r * freqs_sin + xq_i * freqs_cos
xk_out_r: Array["B, L or 1, KVHN, HD//2"] = xk_r * freqs_cos - xk_i * freqs_sin
xk_out_i: Array["B, L or 1, KVHN, HD//2"] = xk_r * freqs_sin + xk_i * freqs_cos

xq_out: Array["B, L or 1, QHN,  HD//2, 2"] = np.stack([xq_out_r, xq_out_i], axis=-1)
xk_out: Array["B, L or 1, KVHN, HD//2, 2"] = np.stack([xk_out_r, xk_out_i], axis=-1)
xq_out: Array["B, L or 1, QHN,  HD"] = xq_out.reshape(xq_out.shape[:-2] + (-1,))
xk_out: Array["B, L or 1, KVHN, HD"] = xk_out.reshape(xk_out.shape[:-2] + (-1,))

원래 트랜스포머에는 QKV로 쪼개기 전에 Position Encoding을 적용하지만 라마는 QKV로 분리한 이후에 Q와 K에만 RoPE를 적용한다.

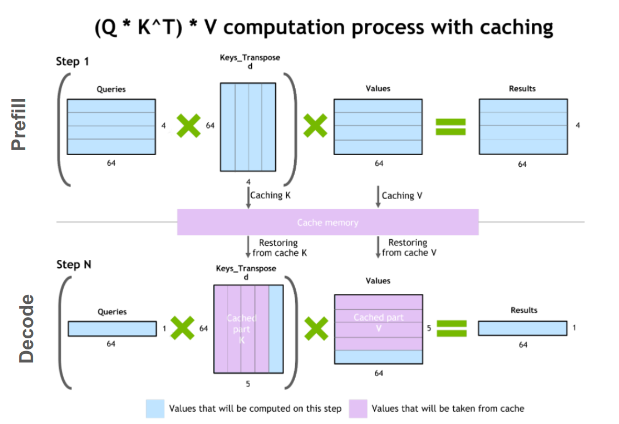
KV Cache

3

GPT 스타일의 생성 모델은 Masked Attention이기 때문에 KV Cache가 가능하다. 뒤에 무슨 단어가 나오든 이후 단어는 보지 못하도록 되어 있으니 이전 결과는 항상 동일할 수밖에 없기 때문이다. 따라서 K와 V는 캐시 하여 활용할 수 있으며 Q 또한 마지막 값만 계산하면 된다. 캐시는 max_seq_len(256)만큼 잡아뒀기 때문에 계산 결과를 집어넣은 다음 다시 현재 length 만큼만 추출해 가져온다.

# KV Cache
self.cache_k[:B, start_pos: start_pos + L] = xk
self.cache_v[:B, start_pos: start_pos + L] = xv
ks: Array["B, L, KVHN, HD"] = self.cache_k[:B, : start_pos + L]
vs: Array["B, L, KVHN, HD"] = self.cache_v[:B, : start_pos + L]
# (1, 256, 6, 48) -> (1, 5, 6, 48)

# GQA
xk: Array["B, L, HN, HD"] = repeat_kv(ks, self.n_rep)
xv: Array["B, L, HN, HD"] = repeat_kv(vs, self.n_rep)

xq: Array["B, HN, L or 1, HD"] = xq.transpose(0, 2, 1, 3)
xk: Array["B, HN, L, HD"] = xk.transpose(0, 2, 1, 3)
xv: Array["B, HN, L, HD"] = xv.transpose(0, 2, 1, 3)

여기서는 캐시 값을 꺼내온 다음 다시 transpose해서 shape을 변경했지만 이 과정을 생략하면 좀 더 효율적으로 처리할 수 있을 것 같다. 참고로 KV Cache의 최대 크기는 배치 1일 때 \(1 \times 256 \times 6 \times 48 \times 2 \times 6 = 884K\)이다. 15M 모델이므로 메모리의 약 6% 정도를 추가로 차지한다고 볼 수 있다.

GQA(Grouped-Query Attention)

4

Multi-query인 MQA는 Multi-head인 MHA에 비해 간결하고 메모리를 절약할 수 있다는 장점이 있지만 성능 저하가 심하고, 학습이 불안정한 문제가 있다. 이에 따라 라마 2부터는 Grouped-query인 GQA가 도입됐다. 라마 2에서는 70B에만 GQA가 적용되어 있지만 라마 3부터는 8B 이상 모든 모델에 GQA가 적용됐다. 여기서는 기존에 GQA 없이 학습한 모델을 사용하기 때문에 GQA를 쓰진 않지만 코드에는 모두 구현해 두었다. 간단히 배수만큼 복사하는 형태로 구현했으며, 추후 최적화를 위해 이전 값을 참조하는 형태로 개선할 수 있다. n_rep==1일 때 GQA를 사용하지 않도록 했다.

if n_rep == 1:
    return x
z: Array["B, L, QHN, HD"] = np.repeat(x, n_rep, axis=2)

Scaled Dot-Product Attention

어텐션은 Multi-Head에서 각각 별도로 계산한다.

\(Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d_k}})V\)

# Scaled Dot-Product Attention
# ["B, HN, L or 1, HD"] @ ["B, HN, HD, L"] -> ["B, HN, L or 1, L"]
attention: Array["B, HN, L or 1, L"] = xq @ xk.transpose(0, 1, 3, 2) / math.sqrt(self.head_dim)
# `mask` is used only once at the beginning.
if mask is not None:
    attention = attention + mask[None, None, :, :]
attention = softmax(attention)
output: Array["B, HN, L or 1, HD"] = attention @ xv

masking은 처음에만 진행하고 이후에는 마지막 Q만 처리하면 되므로 masking이 필요 없다. 이후 softmax와 matmul로 결과를 얻을 수 있다. 최종적으로 Multi-Head 계산 결과는 다음과 같이 전체 dim으로 reshape하여 헤드를 합치고 한번 더 matmul을 해준다.

# ["B, HN, L or 1, HD"] -> ["B, L or 1, D"]
output: Array["B, L or 1, D"] = output.transpose(0, 2, 1, 3).reshape(B, L, -1)
output: Array["B, L or 1, D"] = output @ self.o_weight

QKV 전체를 한꺼번에 계산하는 것은 Prefill 단계에서만 진행된다. 이때 TTFT(Time To First Token)를 Prefill Latency라 하며, 이후 디코드 단계부터는 벡터 @ 행렬 연산만 진행하면 된다. Flash Attention 또한 Inference시에는 Prefill Latency를 줄일때만 효과가 있으며 입력이 길어야 어느정도 성능을 발휘한다.

Feed Forward

라마에서 Feed Forward는 matmul만 진행하는 3개의 linear를 사용하며 bias가 없다. 따라서 GPT와 달리 완전한 fc layer로 보기 어렵다. silu 결과로 swish 값을 만들어서 D에서 FD로 up-scaling한 x_V와 곱하고 다시 down-scaling한다. 여기서 FD의 크기는 FD = 2 * 4 * D / 3이다. 즉 D(288)이므로 FD(768)이다.

swish: Array["B, L or 1, FD"] = silu(x @ self.gate_weight)
x_V: Array["B, L or 1, FD"] = x @ self.up_weight
x: Array["B, L or 1, FD"] = swish * x_V
x: Array["B, L or 1, D"] = x @ self.down_weight

SwiGLU

논문에서 SwiGLU 수식은 다음과 같다.

1

swish와 x_V를 곱하고 W_2와 matmul한 것을 SwiGLU라 하는데 이처럼 3개의 다중 Feed Foward를 활용한 독특한 조합인 SwiGLU는 모델의 성능을 높인다. x는 대략 \(-14 \sim 11\) 사이의 실수값이며 이 값이 silu 함수의 입력이 된다. silu 구현은 다음과 같다.

x * (1 / (1 + np.exp(-x)))

Linear

모든 트랜스포머 블럭을 통과한 후 최종 아웃풋은 속도를 높이기 위해 마지막 logit만 matmul로 계산한다. 애초에 트랜스포머 블럭에는 Prefill 단계 이후에는 항상 ["1, D"]가 결과로 출력된다.

# ["B, 1, VS"] = ["B, 1(L), D"] @ ["D, VS"]
logit: Array["B, 1, VS"] = h[:, [-1], :] @ self.lm_head_weight

생성

이제 이렇게 추출한 logit을 이용해 토큰을 차례대로 생성하는 과정이다. 여기서는 간단한 구현을 위해 생성 과정에서 샘플링을 생략했으며 Greedy 결과만 출력하도록 했다.

for i, curr_pos in enumerate(range(L, max_new_tokens)):
    if i == 0:  # Prefill Phase
        inputs = input_ids
        pos = 0
    else:       # Decode Phase
        inputs = next_id
        pos = curr_pos
    logits: Array["B, 1, VS"] = self(inputs, pos)
    next_id = logits[:, -1, :].argmax(-1, keepdims=True)
    yield next_id

첫 단계는 Prefill 또는 간혹 Summarization이라 부르는 과정(Phase)이다. 여기서는 모든 입력을 전달하며 위치도 0에서 시작한다. Flash Attention이 성능을 발휘하는 구간이기도 하다.

이후부터는 Decode Phase이며 KV Cache 덕분에 마지막 토큰 ID 1개만 Q로 전달하고 결과 또한 최종 logit 1개만 받아온다. 여기서는 샘플링을 생략하고 최댓값만 추출하도록 했다. 만약 샘플링 과정을 추가한다면 softmax를 취하고 top_p와 top_k를 구현하면 된다.

이제 이렇게 생성한 토큰 ID를 결과로 yield하고, 다음 스텝에서는 디코딩해서 토큰을 출력하면 모든 과정을 마무리할 수 있다.

실행

다음과 같이 실행 가능하다.

$ python llama3.py "I have a dream"
"""
I have a dream. He dream of a big, beautiful garden full of flower and tree. He dream of playing with hi friend and eating yummy snack.
One day, he wa walking in the garden when he saw

Token count: 50, elapsed: 1.53s, 33 tokens/s
"""

카파시가 어느 정도 학습을 진행한 모델이다 보니 의미가 이해될 정도로 그럭저럭 괜찮은 문장이 결과로 잘 출력된다. M2 맥북 에어에서 33 tokens/s 속도로 실행됐다.

코드

실행 가능한 전체 코드는 likejazz/llama3.np에서 확인할 수 있다.

References

  1. https://medium.com/@vi.ai_/exploring-and-building-the-llama-3-architecture-a-deep-dive-into-components-coding-and-43d4097cfbbb ↩ ↩2

  2. https://mathworld.wolfram.com/RotationMatrix.html ↩

  3. https://developer.nvidia.com/blog/mastering-llm-techniques-inference-optimization/ ↩

  4. https://arxiv.org/abs/2305.13245 ↩

is a collection of Papers I have written.
© 2000 - Sang Park Except where otherwise noted, content on this site is licensed under a CC BY 4.0.
This site design was brought from Distill.