나이브 베이즈 알고리즘 확률 모델

2018년 3월 6일 베르누이 모델 추가
2017년 3월 24일 초안 작성

• 본론
  • 나이브 베이즈 모듈
  • 뉴스 분류
  • 확률 모델
    • 다항 분포 나이브 베이즈
    • 베르누이 나이브 베이즈
• 정리

본론

나이브 베이즈 모듈

scikit-learn의 나이브 베이즈 모듈인 sklearn.naive_bayes는 총 3가지 나이브 베이즈 분류기를 제공한다.

1. Gaussian Naive Bayes
2. Multinomial Naive Bayes
3. Bernoulli Naive Bayes

이 중 연속적인 값을 지닌 데이터를 처리하는 용도로 가우스 분포를 활용하는 가우시안을 제외한, 문서 분류에 사용하는 다항 분포^Multinomial와 베르누이^Bernoulli모델을 살펴보고 실제로 알고리즘을 계산하면서 검증해보도록 한다.

참고로 알고리즘의 계산 결과는 주피터 노트북에서 확인할 수 있다.

뉴스 분류

먼저, 캐글(Kaggle)의 뉴스 데이타를 이용, 뉴스 제목으로 카테고리를 분류하는 실험을 진행해봤다. 평가가 가장 좋았던 커널을 fork하여 하나씩 진행해보니 랜덤 포레스트에서 84%를 기록. 디시젼 트리만 해도 80%가 넘는 나쁘지 않은 수치를 기록했다. CNN 딥러닝이 80% 언저리에서 계속 고전했던걸 생각해보면 훨씬 빠르게 유사 혹은 능가하는 정확도를 기록한 셈이다. 놀랍게도 다항 분포 나이브 베이즈는 90%가 넘는 정확도를 기록했는데 속도 또한 다른 알고리즘과 비교가 안될 정도로 빠르다.

나이브 베이즈 간 비교도 진행을 했고 연속적인 데이터를 처리하는 용도로 성격이 다른 가우시안을 제외한, 다항 분포와 베르누이가 비슷한 성능을 보였고 다항 분포가 근소한 차이로 더 나은 성능을 보였다. 물론 이는 데이타의 특성이 반영된 결과로 다항 분포가 항상 좋은건 아니다. 그러나 18세기에 등장한 이 간단한 수식이 21세기에도 여전히 최고의 알고리즘 이라는 사실에는 그저 놀라울 따름이다.

확률 모델

먼저 테스트 값을 정의하고 scikit-learn 나이브 베이즈 모듈의 공통 프로퍼티를 정리했다. 각 프로퍼티는 가우시안, 다항 분포, 베르누이 모두 공통으로 사용하며 _count_ 접미사의 값(당연히)과 사전 확률 class_log_prior_는 모두 동일하다.

주피터 노트북에서 사용한 학습 데이터를 기준으로 프로퍼티를 정리하면 아래와 같다.

다항 분포 나이브 베이즈

다항 분포 나이브 베이즈의 수도^pseudo 코드는 Introduction to Information Retrieval(Manning et al., 2008) 책 챕터 13에 잘 나와 있다.

이 책은 전문이 PDF 형태로 온라인에 무료 공개 되어 있으며 직접 확인할 수 있다.

다항 분포의 각 특징 확률. 즉, feature_log_prob_는 X의 갯수를 X의 합으로 나눈 값에 라플라스 스무딩(default: 1)을 적용해 로그를 취한 결과로 아래와 같다.

np.log((fc + clf.alpha) / (np.repeat(fc.sum(axis=1)[:, np.newaxis],
4, axis=1) + clf.alpha * X.shape[1]))
--
array([[-1.54044504, -1.02961942, -1.25276297, -1.94591015],
       [-1.73460106, -1.44691898, -1.04145387, -1.44691898]])

확률 \(P(t_k \mid c)\)의 최대 사후 클래스 수식은 아래와 같다.

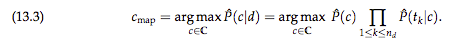
이 수식은 여러 조건부 확률 \((P(t_k \mid c),1 \leq k \leq n_d)\) 을 곱하므로 실수형 계산에서 언더플로우 현상이 발생할 수 있다. 딥러닝에서도 유사하게 기울기 소실 문제^{Vanishing Gradient Problem}가 있는데, 이 문제를 개선하기 위해 딥러닝에서는 값을 크게하는 ReLU를 적용하였고, 여기서는 각 조건부 확률의 로그 값을 취해 곱하기 대신 더하기를 사용해 해결한다. (Manning et al., 2008)

다항 분포의 예측 결과 확률 predict_proba는 아래와 같다.

log_p = clf.class_log_prior_ + np.sum(clf.feature_log_prob_ * x_new, axis=1)
np.exp(log_p) / np.sum(np.exp(log_p))
--
array([0.55131629, 0.44868371])

각 조건부 확률^likelihood의 로그 합이며, 이를 백분율로 환산하여 보여준다. 베이즈 룰 수식과 달리 분모. 즉, 증거^evidence를 사용하지 않는데, 이는 모든 클래스에 대해 항상 같은 값을 갖기 때문이며 \(argmax\)에 아무런 영향을 끼치지 않기 때문이다. 나이브 베이즈가 성공적인 이유는 사후 확률의 우수함이 아니라 \(argmax_y{P(Y \rvert X)}\) 의 우수함 때문이라 말하며(Domingos, Pazzani, 1997) 이는 확률 추정은 좋지 않지만 성능이 뛰어난 이유를 잘 설명한다.

다항 분포 나이브 베이즈로 문장의 카테고리 분류를 예측한 결과

베르누이 나이브 베이즈

다항 분포와 달리 베르누이는 출현 여부로 확률을 계산한다.

feature_log_prob_는 아래와 같이 피쳐의 총합이 아닌 클래스의 총합에 라플라스 스무딩의 2배수를 분모로 한다.

np.log((clf_bern.feature_count_ + 1) / \
       (clf_bern.class_count_.reshape(-1, 1) + 2))
--
array([[-0.69314718, -0.18232156, -0.40546511, -1.09861229],
       [-0.98082925, -0.69314718, -0.28768207, -0.69314718]])

마찬가지로 IIR 책의 수도 코드를 구현하였으며, 실제로 scikit-learn의 내부^internal 코드를 보면 IIR 책을 참조했다는 주석이 달려 있다. 테스트 케이스에도 책에서 제시한 값과 동일한 테스트가 여럿 등록되어 있다.

아울러 다항 분포와 달리 출현하지 않은 토큰에 대해서도 출현하지 않을 확률 즉, log(1-condprob[t][c])을 반영 한다는 차이점이 있다.

neg_prob = np.log(1 - np.exp(clf_bern.feature_log_prob_))
log_p_bern = clf_bern.class_log_prior_ + \
np.sum(clf_bern.feature_log_prob_ * x_new + \
       neg_prob * (1 - x_new), axis=1)
np.exp(log_p_bern) / np.sum(np.exp(log_p_bern))
--
array([0.72480181, 0.27519819])

출현 빈도^occurrences를 반영하는 다항 분포와 다르게 베르누이의 확률 값은 다르게 나온다. 하지만 판별 값은 여전히 동일하다. 앞서 언급한 것 처럼 나이브 베이즈는 확률 추정은 정교하지 않지만 판별 성능은 뛰어나기 때문이다.

베르누이는 수십개 이하의 작은 모델로도 상당한 성능을 보이며, 개념 이동^{concept drift}(예를 들어 미국의 대통령이 오바마에서 트럼프로 변한 것 같은)에도 잘 적응한다. 다만, 빈도 수를 반영하지 않으므로 이 같은 특성에 따른 적절한 모델을 잘 선택하는 것이 중요하다.

정리

계산을 직접 진행하여 검증한 주피터 노트북은 각각 아래와 같다.

• 나이브 베이즈 확률 모델 계산
• 뉴스 카테고리 분류 실험
• 뉴스 카테고리 분류 나이브 베이즈 간 비교 실험