딥러닝

개요
경사 하강법Gradient Descent
성능
미분
최적화Optimization
기울기Gradient
- 기울기 소실Gradient Vanishing
배치 정규화Batch Nomarlization
가중치 감소Weight Decay
bfloat16

개요

프로그래머들이 명시적인 규칙을 충분하게 많이 만들어 지식을 다루면 인간 수준의 인공 지능을 만들 수 있다고 믿었습니다. 이런 접근 방법을 심볼릭 AI ^{symbolic AI}라고 하며 1950년대부터 1980년대까지 AI 분야의 지배적인 패러다임이었습니다. 1980년대 심볼릭 AI의 새로운 버전인 전문가 시스템 ^{expert system}이 큰 기업들 사이에서 인기를 끌기 시작했습니다. (케라스 창시자에게 배우는 딥러닝, 2017)

초창기에 인공지능 학계는 두 진영으로 분열되었다. 한쪽은 이른바 규칙 기반 또는 상징적 인공지능을 추구했다. 다른 한쪽은 통계적 패턴 인식 시스템을 구축했다. 전자는 성인이 외국어를 배우려고 노력하는 방식으로 인공지능에 접근하려고 시도했다. 후자는 아이가 첫 언어를 배우는 것과 흡사한 방식으로 인공지능을 구축하려고 시도했다. (머신 플랫폼 크라우드, 2017)

경사 하강법^{Gradient Descent}

수식 $f(x)=x^4-3x^3+2$ 은 상기 미분 그래프를 보면 0에 local minima, 2.25에 global minima가 있다. (위키피디어) 경사 하강법으로 minima를 찾는 알고리즘은 아래와 같다.

x_old = 0
x_new = 6
eps = 0.01
precision = 1e-5
step = 1

def f_prime(x):
    return 4*x**3-9*x**2

while abs(x_new - x_old) > precision:
    x_old = x_new
    x_new = x_old - eps * f_prime(x_old)
    print('#%d x_old:%f, x_new:%f, grad:%f, diff:%.8f' % (step, x_old, x_new, f_prime(x_old), (x_new - x_old)))
    step += 1

print("Minimum occurs at %f" % x_new)

약 70여회 반복 후 2.25를 찾아낸다.

...
67 x_old:2.249913, x_new:2.249930, grad:-0.001772, diff:0.00001772
68 x_old:2.249930, x_new:2.249944, grad:-0.001413, diff:0.00001413
69 x_old:2.249944, x_new:2.249956, grad:-0.001127, diff:0.00001127
70 x_old:2.249956, x_new:2.249965, grad:-0.000899, diff:0.00000899
Minimum occurs at 2.249965

물론 이 경우 초기값이 0보다 작다면 local minima인 0에 빠지게 된다.

성능

행렬 크기가 너무 작아 256 중간 노드를 4096으로 키웠는데, 맥북 프로에서 126s 걸리던 작업이 P40 GPU에서 3.8s로 무려 30배 이상의 성능 개선이 있다. 행렬 사이즈가 작으면 별다른 차이점이 없지만 행렬이 충분히 크면 GPU에서 개선된 속도를 보여준다.

타입	노드	epoch	성능
맥북 프로	256	5000	20s
	4096	5000	239s
Tesla P40	256	5000	8.5s
	4096	5000	11.26s

미분

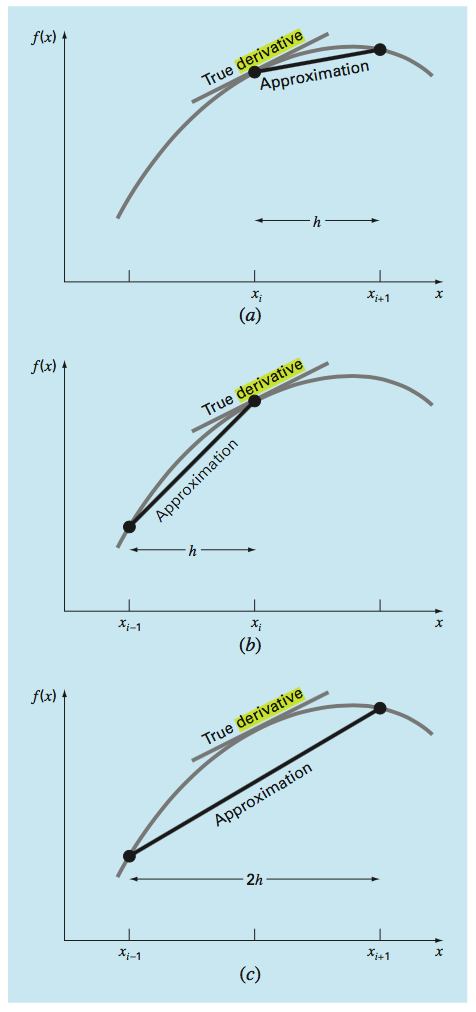
(Numerical Methods for Engineers, 2009)

(a)전진차분, (b)후진차분, (c)중앙차분^{Centered Finite-Divided-Difference}의 표현 비교. 중앙차분이 실제미분과 가장 가까운 것을 확인할 수 있다.

\[f^{'}(x){\approx}{\frac{f(x+h)-f(x-h)}{2h}}\]

수치 미분의 h 즉, ${\delta}$ 값은 0.0001(1e-4)로 지정. 범위가 클수록 해석적 미분의 값과 차이가 난다. cs231n의 만족스러운 기준은 1e-7이라고(맞추기 어렵다)

최적화^Optimization

GD vs. SGD

Sebastian Raschka의 답변에 따르면, GD는 1 epoch 동안 모든 트레이닝셋에 대한 gradients의 sum이다. 수식이 mean이 아니라 sum인데, 생각해보면 어차피 음수도 나오고 양수도 나오기 때문에 sum으로 인한 문제가 없다. 배치 단위로 업데이트 하기 때문에 batch GD라고도 불린다.

SGD는 샘플 단위로 gradients를 업데이트 한다. stochastic이라는 용어는 통계학에서 쓰이는 확률론적 근사 ^{stochastic approximation}에서 따왔다고 한다. 이런 ‘확률론적’ 특성 때문에 GD 처럼 global minima에 직접 나아가진 않지만 지그재그 형태로 접근하게 되며, cost function이 convex 형태라면 SGD 또한 충분히 global minima에 잘 수렴한다. (Bottou, Léon, 1998)

그리고 several different flavors of SGD로 shuffling에 대해 언급한다. 즉, 랜덤 샘플링은 일종의 SGD의 변종(variants)인 셈이다. 세가지 경우를 언급하는데 요점은 같다. 섞어주고 매 번 다른 데이터 batch가 들어가게 한다. TensorFlow에도 next_batch() 메소드는 shuffle=True가 디폴트 옵션으로 되어 있으며 매 배치시 데이터가 섞여서 유입된다.

MINI-BATCH는 일정 개수의 샘플을 묶어서 사용한다. 일반적인 미니 배치 사이즈는 k=50이며, 50 묶음 트레이닝 샘플 단위로 gradients 업데이트를 한다.

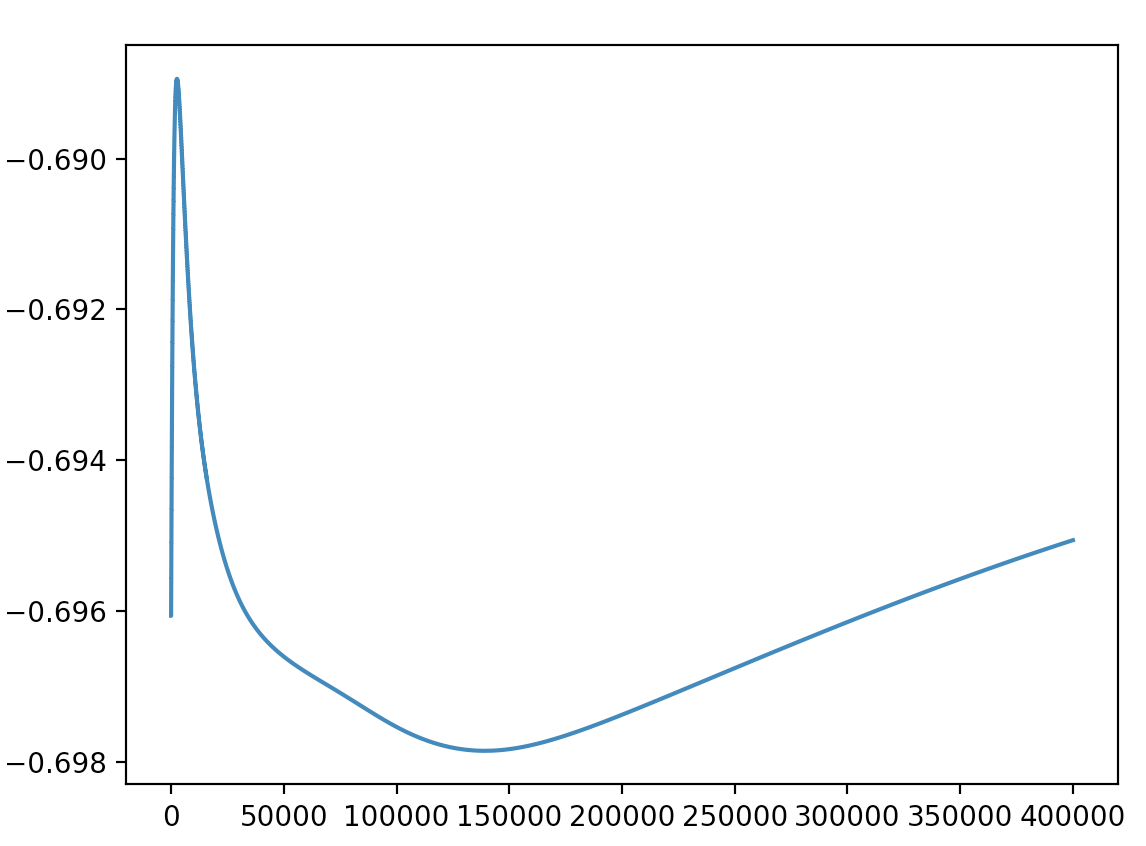
SGD로 학습할때 $w_{1950}$ (임의의 가중치)의 값 변화 그래프

GD 기반의 다양한 최적화 알고리즘을 Sebastian Ruder(!)가 정리.

AdaGrad

학습률을 자동적으로 결정하는(변형하는) 방법으로 가장 많이 사용된다. (딥러닝 제대로 시작하기, 2015) 이전 기울기의 제곱합의 제곱근을 분모로 하여 학습률을 점점 낮춘다.

최적화 발달 계보

(source)

기울기^Gradient

경사 하강법의 기울기 업데이트 수식은 아래와 같다.
$w_i\leftarrow w_i-\eta\frac{\partial E}{\partial w_i}$

${\Delta}w$ 수식은 Delta rule로 정리되어 있다.
${\Delta}w_i=-\eta\frac{\partial E}{\partial w_i},$

Delta rule에서 구하기 가장 까다로운 부분은 $y_j$ 즉, actual output이며, 이유는 이전 레이어로 깊이 내려갈수록 편미분을 하기 위해 수식을 계속 풀어헤쳐야 해서 점점 더 복잡해지기 때문이다. 행렬 연산을 이용하면 출력 레이어 부터 꾸준히 에러를 누적해 나갈 수 있으며, 이 부분이 역전파의 핵심이라고 생각한다. 기본적으로 구하고자 하는 가중치의 출력 노드 다음 노드의 activation 미분과 이전 가중치를 꾸준히 곱해 나가면 된다.

기울기 소실^{Gradient Vanishing}

신경망이 깊을때 활성화 함수를 통한 기울기 값 0 ~ 1은 매우 작은 값이고 역전파^{Backpropagation}중에 배가되어 깊은 망에서 소실^Vanishing되는 효과를 가져온다. ReLU와 LSTM 아키텍처를 사용하여 해결하는 방법이 일반적이다.

배치 정규화^{Batch Nomarlization}

학습을 빨리 진행할 수 있다.
초깃값에 크게 의존하지 않는다.
오버피팅을 억제한다.

가중치 감소^{Weight Decay}

오버피팅을 줄이기 위해 큰 가중치에 대해 L2 norm을 이용한 페널티를 준다.

\[\widetilde{E}(\mathbf{W})=E(\mathbf{W})+\frac{\lambda}{2}\mathbf{W}^2\]

에러 펑션에 L2 정규화^{L2 Regularization} $W={\sqrt{W_1^2+W_2^2+...+W_n^2}}$ 를 추가 했다. (밑바닥부터 시작하는 딥러닝, 2016)

경사 하강법에 가중치 감소를 적용한 새로운 비용 함수 (ref)
(개별 가중치 $w_i$를 업데이트 할 경우에 대한 수식)

\[w_i{\leftarrow}w_i-\eta\frac{\partial{E}}{\partial{w_i}}-\eta\lambda{w_i}\]

큰 가중치에 페널티를 주고 효과적으로 모델을 제한한다.

${\eta}$: 학습률^{learning rate}
${\lambda}$: 정규화 파라미터

overfitting을 피하는 처리 과정을 규제 ^{regularization}라고 한다. L2 regularization의 경우 동일한 파라미터 수를 갖고 있더라도 사용한 모델이 기본 모델 보다 훨씬 더 overfitting에 잘 견딘다. val loss가 반대 방향으로 거의 증가하지 않음. (케라스 창시자에게 배우는 딥러닝, 2017)

bfloat16

FP32와 지수부 exponent는 동일해 range는 넓히고, 가수부 mantissa는 줄여서 정확도는 낮춤. underflow를 줄이는 대신 정확도를 낮춘다. IEEE-754 부동 소수점 FP32 테스트 A100부터 GPU에서 지원한다.

https://cloud.google.com/tpu/docs/bfloat16 ↩

Last Modified: 2023/09/24 00:39:42

딥러닝

개요

경사 하강법Gradient Descent

성능

미분

최적화Optimization