머신러닝

Research v Production
데이터 과학
Improving ML inferences
차원 축소Dimensionality Reduction: PCA
Markov Chains
Grid Search
Scaling, Normalization, Standardization
정보 이론
단순성의 원리
링크

Research v Production

	Research ML	Production ML
데이터	고정(Static)	계속 변함(Dynamic - Shifting)
중요 요소	모델 성능(acc, RMSE)	모델 성능, 빠른 Inferencing, 해석 가능성
도전 과제	더 좋은 성능을 내는 모델, 새로운 구조의 모델	안정적인 운영, 전체 시스템 구조
학습	고정 데이터에 기반한 모델 구조, 파라미터 기반 재학습	시간의 흐름에 따라 데이터 변경 재학습
목적	논문 출판	서비스 문제 해결
표현	offline	online

데이터 과학

Improving ML inferences

차원 축소^{Dimensionality Reduction}: PCA

PCA는 회전된 특징이 통계적으로 상관 관계가 없도록 데이타셋을 회전시키는 방법이다. 상관도가 높은 변수를 통합한다는 점에서 차원 축소^{dimensionality reduction} 기법이라 한다. feature를 선별하는 것과 함께 feature engineering(extraction) 범주에 포함된다.

PCA(whiten=True): This is the same as using StandardScaler after the transformation. whitening corresponds to not only rotating the data, but also rescaling it.

속성 추출 기법

선형 PCA^{principal component analysis} 선형 제한
비선형 MDS^{multidimensional scaling}

PCA 주로 성분 분석

데이터에서 평균값 빼서 데이터를 중심에
공분산^covariance 매트릭스 계산
공분산의 고유벡터^eigenvector 계산

Markov Chains

시각화 제공 이외에도 여러 시각 자료가 있는데 멋진 구현

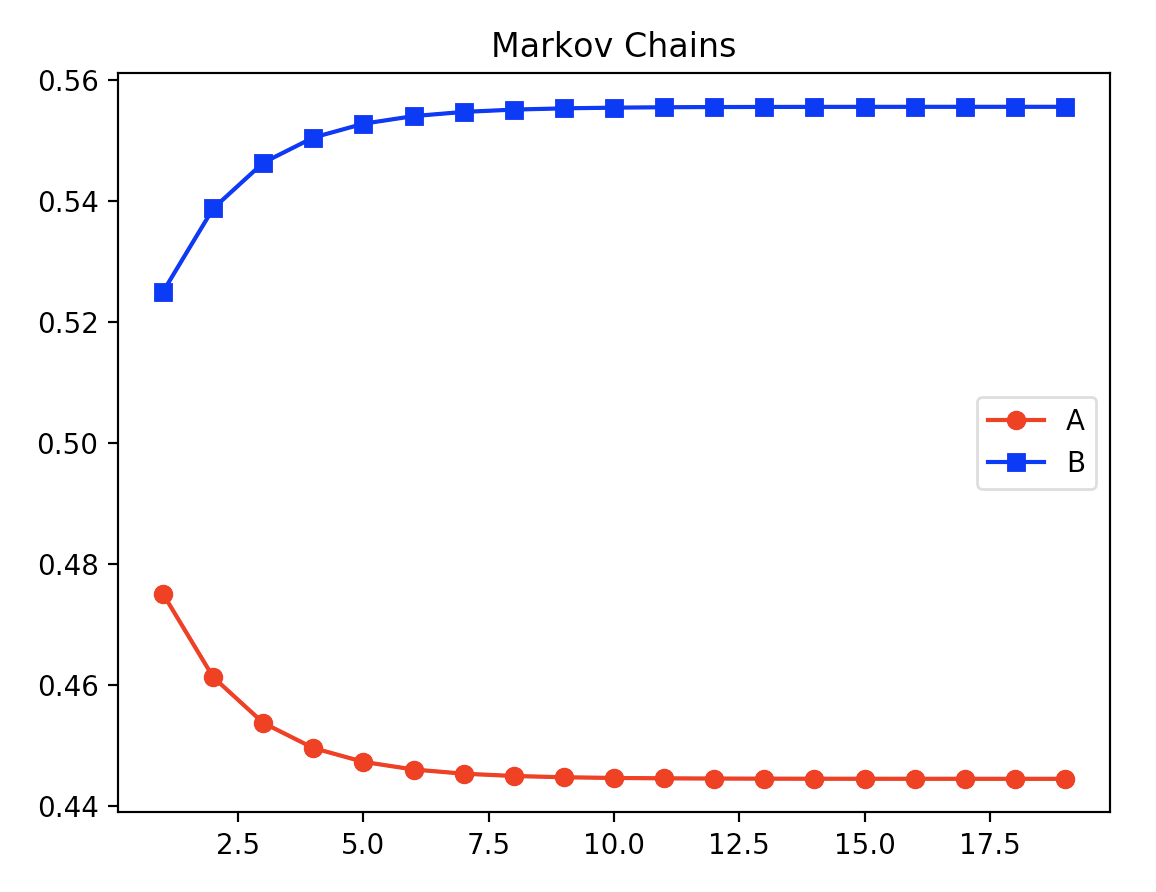
마코프 체인의 결과는 일정 비율로 수렴한다.

Grid Search

하이퍼 파라미터를 결정하기 위해 다양한 파라미터로 실험을 진행해 최적의 파라미터를 찾는 과정이다. scikit-learn의 Grid Search 문서에 잘 정리되어 있다.

Scaling, Normalization, Standardization

Scaling: 서로 다른 단위의 데이터를 같은 단위로 만들어서 큰 숫자가 더 중요해보이는 왜곡을 막는 것
Standardization(= z-score normalization): 분포를 평균 0, 표준편차 1로 바꾸는것
Normalization(= Min-Max scaling) : 변수를 0과 1사이로 바꾸는것

스케일링을 위한 노말라이제이션을 스탠다더라이제이션으로 할 수 있어서 구분이 어렵습니다. ⁴

정보 이론

정보량은 불확실성과 직접적 관련이 있다. 매우 불확실한 일이나 전혀 모르는 일을 이해하려면 많은 정보를 파악해야 한다. 반대로 이미 많이 알고 있는 일은 정보가 많지 않아도 쉽게 이해할 수 있다. 이런 점에서 정보량은 불확실성의 크기와 같다고 볼 수 있다.

(Information) Entropy, in other words, is a measure of uncertainty. ⁵

1948년 클로드 섀넌이 그의 유명한 논문 “A Mathematics Theory of Communication”에 ‘정보 엔트로피’ 개념을 제기하면서 정보의 단위 문제가 풀렸고, 정보의 역할을 계량화 할 수 있게 되었다. (수학의 아름다움, 2014, 2019)

월드컵 32개국 중 우승팀을 맞출 확률은 이진 검색으로 탐색시 5회가 나온다. 그런데 만약 역대 우승국을 중심으로 우승 후보를 미리 추려낸다면 4회 이내가 될 수도 있다. 섀넌의 엔트로피 수식 $H(E)=-\sum_{j=1}^{c}p_j{\log}p_j$ 에 대입하면 마찬가지로 모든 팀의 우승 확률이 동일할 경우 Information Entropy는 5비트가 되지만 만약 어느 한 팀의 우승 확률이 높다면 엔트로피는 5비트 미만으로 낮아질 수 있다는 식이다. (수학의 아름다움)

단순성의 원리

뉴턴의 제1법칙: 관성의 법칙
물체의 질량 중심은 외부 힘이 작용하지 않는 한 일정한 속도로 움직인다.
우쥔은 이를 단순성의 원칙이라 표현했다.
오컴의 면도날(Occam’s Razor 또는 Ockham’s Razor)

simpler solutions are more likely to be correct than complex ones
단순한 솔루션이 복잡한 솔루션 보다 정확할 가능성이 높다.

링크

Last Modified: 2023/04/13 14:13:50