통계학 응용
읽어볼만한 링크
- 유의성 검증Tests of Statistical Significance
‘가설검정’ P값, 더 이상 전가의 보도 아니다, 실험 재현성의 위기 읽어보기
p-value의 헛점, ‘승자의 저주’, ‘데이터를 고문해서 자백 받아내기’에 대한 비슷한 지적을 하는 컬럼이다. 『틀리지 않는 법』에서 얘기한 ‘추론Inference‘의 함정은 모수가 크면 잘못된 추론을 할 수 있다. 선택 편향Selection Bias에 빠지게 된다. 선택 편향은 표본을 사전 또는 사후 선택함에 따라 통계 분석을 왜곡하는 오류다. - 탐색적 데이타 분석EDA: Exploratory Data Analysis
시각적 방법을 사용하여 주요 특성을 요약하기 위해 데이터 집합을 분석하는 방법 - 선형성Linearity에 함정이 있다고 얘기한다. 실제로는 선형이 아닌 데이타를 선형으로 잘못 인식한다는 것.
카드 한 벌을 완벽하게 잘 섞으려면 셔플을 7번 해야 한다. (뉴욕타임스 수학, 2013, 1990년 기사)
야간병동의 수상한 죽음들: 통계보다 훨씬 더 많은 수의 환자가 죽는 것을 통해 죽음의 천사의 존재를 밝혀내다. (넘버스, 2017)
피셔가 쓴 『Statistical Methods for Research Workers』의 많은 부분에서 p-value를 어떻게 계산하는지 보여주는데 전념한다. (p110 차를 맛보는 여인 2001, 2019)
이론 및 사례
보렐Emile Borel의 법칙
무한 원숭이 정리Infinite monkey theorem 는 무한성에 기초한 원리로, 타자기 앞에 앉아서 마음대로 쳐대는 원숭이가 프랑스 국립 박물관의 모든 책을 언젠가는 쳐낼 가능성이 거의 확실Almost surely, Probability 1하다는 정리다. 즉, \(\lim_{x\rightarrow\infty}{P(x)}=1\) 이다.
모든 가능성을 하나씩 체크해 솔루션을 찾는 접근법으로 BMA(British Museum Algorithm)라고도 한다. (Brute-force or exhaustive search와 유사)
푸아송 분포
런던 대공습의 폭탄이 정밀 타격인지 분석 결과, 푸아송 분포를 따랐다.1 정밀 타격이 아니라고 결론을 내렸다.
1946년, 보험계리사협회의 회원 R.D.클라크는 면적이 144제곱킬로미터인 런던의 지도를 0.25제곱킬로미터 면적의 정사각형 576개로 구획하고, 각각의 정사각형에 떨어진 V-1 비행폭탄의 개수를 세는 방법으로 이 문제에 도전했다. 만일 그 폭탄들이 무작위한 장소에 떨어졌다면, 폭탄이 0개 떨어진 정사각형의 개수, 1개 떨어진 정사각형의 개수, 2개 떨어진 정사각형의 개수 등을 푸아송 분포에 기초하여 대략 예측할 수 있어야 한다. 클라크는 탄착 지점의 의도적 집중은 없었고 따라서 V-1 비행폭탄은 정확히 조준되지 않았다고 결론 내렸다. 사람들의 눈에 띈 탄착 지점 집중은 순전히 폭탄의 수가 많은 것에서 비롯된 현상이었고 우연의 법칙으로 설명할 수 있었다. (신은 주사위 놀이를 하지 않는다, 2014)
다음과 같이 특수한 경우 포아송 분포는 정규분포보다 좋은 근사 결과를 도출해낸다 (p164, 처음 시작하는 만화 통계학, 2012)
- 시행횟수 \(n\)이 엄청나게 크다. 1만 또는 그 이상
- 발생확률 \(p\)가 엄청나게 작다. \(\frac{1}{1000}\) 또는 \(\frac{1}{10000}\)등
- e.g. 교통사고 발생률 등. 경기도는 평균을 내면 매년 한 사람씩 ‘인기 예능인’을 배출하고 있다고 한다. 올해 두 명의 ‘인기 예능인’이 대박을 낼 확률은 어느 정도인가? 0.1839 약 18%
- \(n\)이 얼마든 관계없다. 몰라도 가능
from scipy.stats import poisson poisson.pmf(2, 1) # 0.18393972058572114
- \(n\)이 얼마든 관계없다. 몰라도 가능
빈도주의자 vs 베이즈주의자
빈도론파는 단순하게 생각한다. 동전을 10번 던져 10번 모두 앞면이 나왔다면 이 동전이 진짜 동전이라고 말할 수 있을까. \(\frac{1}{2}^{10}\) 확률이므로 p-value는 0.1%이다. 따라서 ‘생각하기 어렵다’며 버리는 편이 합당하다. 80% 확률로 앞이 나오는 가짜 동전이라면 p-value는 10.74%다. 따라서 이 가정은 완전히 버릴 수 없다.
베이즈파는 아무 정보도 없는 시점에서 사전확률을 설정한다. 마찬가지로 진짜와 가짜일때 조건부 확률은 동일하게 0.1%. 10.74%이지만, 베이즈론자의 계산 방법은 그 다음부터가 조금 다르다. 베이즈론자는 진짜인 경우와 가짜인 경우 각각의 상황에서 사전확률과 조건부확률의 곱셈을 한다. 따라서 아래와 같은 계산식이 성립한다.
- 진짜의 사전확률 x 진짜인 경우 10번 모두 앞면이 나오는 조건부 확률 = 50% * 0.1% = 0.05%
- 가짜의 사전확률 x 가짜인 경우 10번 모두 앞면이 나오는 조건부 확률 = 50% * 10.74% = 5.37%
- 이후에 1+2 합계인 5.42%로 나눠준다. 즉, 0.05 / 5.42 = 0.90%, 동전이 가짜일 확률은 5.37 / 5.42 = 99.10% 이다. 사전확률과 데이터에 근거해 사후확률을 산출한다.
최초의 사전 확률이 90% 진짜 동전이라 하더라도 90% * 0.1% = 0.09% / (0.09% + 1.07%) = 7.57% 밖에 안되므로 92.43%의 확률로 가짜이고, 사전 확률에 의한 영향은 적다고 주장하고 싶을 것이다. 예를 들어 동전을 3번만 던질 수 있는 상태에서 빈도론은 ‘어느 쪽인지 모른다’는 판단밖에 못하지만, 베이즈론에 의하면 적어도 어느쪽의 가능성이 높은지는 판단할 수 있다. 그래서 실수가 용납되지 않는 보수적 판단이 요구되는 분야일수록 빈도론의 의존하는 경향이 있다. 의료 분야에서 신약 사용을 승인할지 말지의 판단은 가장 실수가 용납되지 않는 영역이다. 오랜 세월 국가 데이터를 만드는 일에 고심해온 사회조사 통계 전문가도, ‘만약 실업률이 3%라면~’등의 가정을 하는 것은 잘못된 정책 결정으로 이어질 수 있기 때문에 베이즈론을 좋아하지 않는다. 본래 대량의 임의 표본에서 올바른 추정치를 얻는 것을 건제로 하는 사회조사 분야에서는 베이즈적 사고방식의 이점은 매우 적다.
한정된 정보와 가정을 조합하는 ‘효율성’이 요구된다면 베이즈론을 사용하면 되고, ‘잘못될 가능성을 줄이고 싶다’거나 ‘충분한 데이터가 확보되어 있다’면 빈도론으로 p-value를 구하는 편이 낫다.
(통계의 힘, 2013)
게임 이론Game theory
게임이론은 전략적인 상황, 즉 다른 사람들이 어떤 결정을 내릴지를 생각해 그것을 바탕으로 자신의 결정을 내릴 때 사람들이 어떻게 행동하는지를 연구하는 수학의 한 영역이다. 일반적으로 게임이론은 사람들이 언제나 합리적이고 이기적이라고 가정한다. (뉴욕타임스 수학, 2013, 2009년 기사) 다이나믹 프로그래밍에서 탐욕 알고리즘과 유사.
큰 수의 법칙Law of large numbers
‘제임스 본드 영화에 나오는 폭탄에 4자리 암호가 있는데, 내 이스라엘 은행 계좌 비밀번호하고 똑같았다’고 말하는 친구가 있다. 네 자리 수는 10,000개나 있기 때문에 그런 우연이 희한하게 들린다. 하지만 디아코니스 박사는 “주민등록번호, 계좌 비밀번호, 친구들의 전화번호 등 120개의 수를 알고 있다면, 그 중 두 가지 수에서 네 숫자가 똑같을 확률은 50%”라고 덧붙였다. (뉴욕타임스 수학, 2013, 1990년 기사)
왼손잡이 문제는 관측된 왼손잡이 비율의 변동성이 표본 크기가 커질수로 작아짐을 보여줬다. 18세기 초반 스위스 수학자 야코프 베르누이 Jacob Bernoulli가 확립한 큰 수의 법칙으로 설명된다. (p264. 숫자에 약한 사람들을 위한 통계학 수업, 2019)
몬티 홀 문제Monty Hall problem
IQ 228로 기네스북에 등재된 메릴린 보스 사반트가 진행하는 ‘사반트에게 물어보세요’ 컬럼에서 몬티 홀 문제에 대한 질문을 받았고, 변경하는 것이 더 유리하다고 답변했다. 많은 논란이 있었으나 결국 변경하는 것이 정답일 확률이 2/3로 더 높음이 밝혀졌다. 물론 이는 사회자가 항상 힌트를 내준다는 가정하에서다. 생일이 겹치는 문제와 함께 확률을 잘못 계산하는 대표적인 문제 (좋은 선택, 나쁜 선택, 2019)
콜레라 역학조사John Snow, 1854
최근접 이웃 알고리즘(kNN)의 성공 사례, 공식적으로 발명 되기 한 세기 전의 일이다.
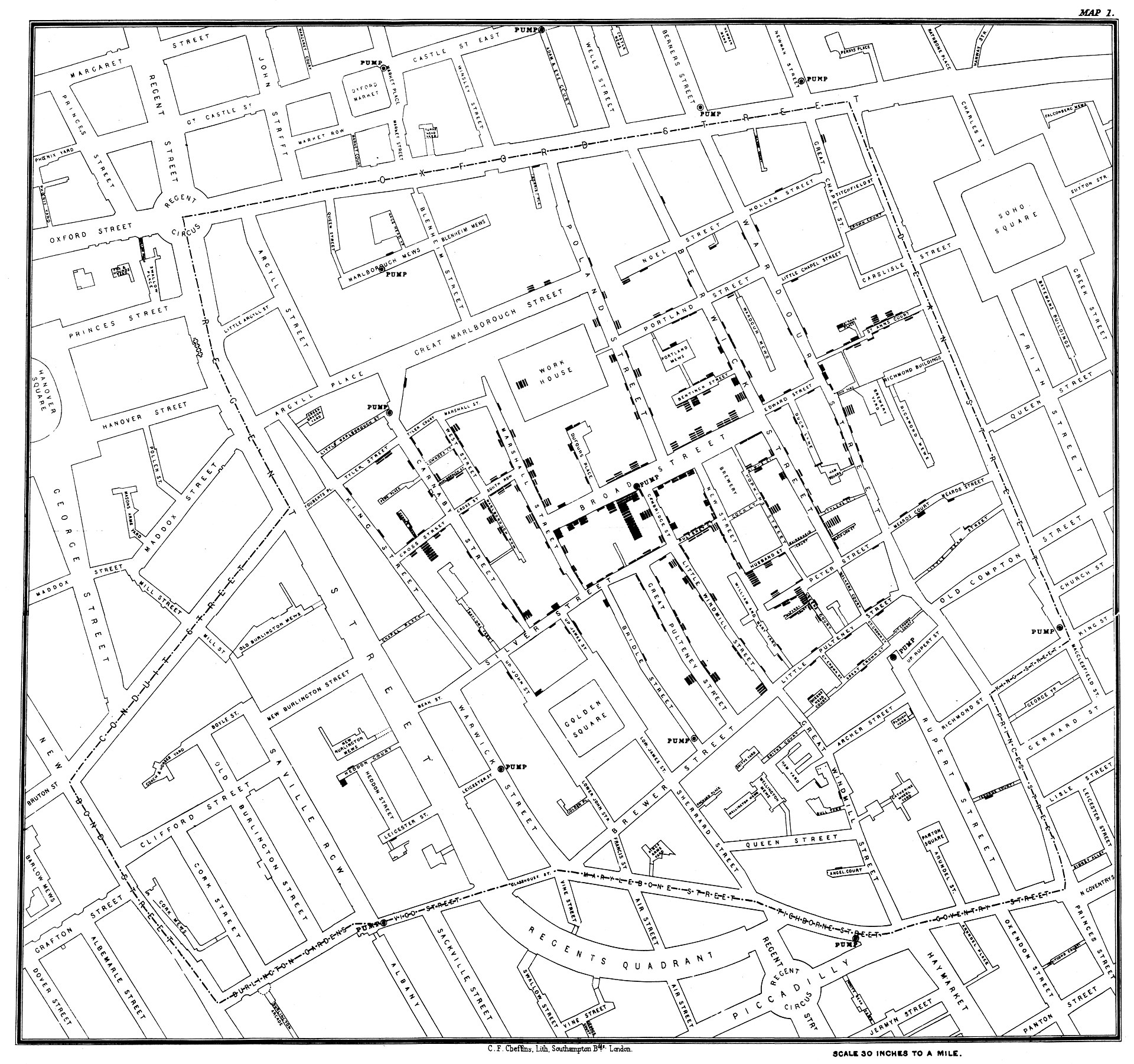
역학 조사의 대표적인 사례는 프래밍험 심장연구Framingham Heart Study로 1948년 심장병의 원인을 밝혀내기 위해 시작됐다. 따라서, 결과가 나오기 전부터 집단을 계속적으로 조사한 역학 연구를 프레이밍험 연구(또는 코호트Cohort 연구) 방식이라고 한다.
분모 무시denominator neglect
- 1번 단지에는 구슬 10개, 하얀 구슬 9개와 빨간 구슬 1개가 있다.
- 2번 단지에는 구슬 100개, 하얀 구슬 92개와 빨간 구슬 8개가 있다.
어느 단지를 택할 것인가. 간단한 계산으로도 1번이 확률이 높다. 그러나 약 3분의 1은 2번 단지를 택한다. 더 많은 구슬이 있기 때문에 더 골고루 섞여 있을 것이라고 추론하기 때문이다. 그러나 다음 단계에서 2번 단지에 더 골고루 섞여 있으므로 거기에서 빨간 구슬을 뽑을 확률이 더 높다는 그릇된 추론을 한다. (신은 주사위 놀이를 하지 않는다, 2014)
벤포드의 법칙 Benford’s law
실세계에 존재하는 많은 수치 데이터의 10진법 값 수의 첫째 자리의 확률 분포를 관찰한 결과, 첫째 자리 숫자가 작을 확률이 크다. (위키피디어, 세계 수학 걸작선, 2017)
넷플릭스 Connected2에서 뉴컴이 로그책을 보면서 발견했다는 얘기, 회계부정(대표적으로 엔론)을 적발하는데 활용했다는 얘기가 나온다. 수학적으로 면밀하진 않지만 쉽게 이해되는 설명으로, 1,000이 2,000이 되려면 100% 증가해야 하지만 9,000이 10,000이 되려면 12%만 증가하면 된다.(Mark J. Nigrini 박사)
F1 Score
F1 스코어 is the harmonic mean조화 평균 of precision and recall:

precision이 50일때 recall 점수 변화에 따른 F1 스코어. recall이 100이면 F1 스코어는 66.6이 된다.
Confusion Matrix
시각화
박스 플롯box and whisker plot
상위Upper Quartile 25%, 중앙값Median, 하위 25%(상위 75%)
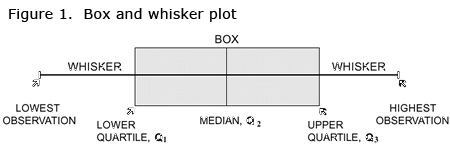
바이올린 플롯: 박스 플롯과 유사하지만 각 면에 커널 밀도를 회전 표시. 직관적일거라 생각했는데 막상 보니 기괴하여 박스 앤 휘스커 플롯에 비해 더 헷갈린다.

(The Data Visualisation Catalogue)
200년 동안 세계의 여러 나라가 어떻게 변했는지를 보여주는 버블 차트
기타
복권을 사재기한 투자 그룹 이야기가 나오는데 『틀리지 않는 법』 에서도 나왔던 얘기다. 1992년 버지니아 주의 로또 복권은 1~44 숫자 가운데 6개를 고르는 규칙이었고 가능한 조합은 44! / 6! * 38! = 7,059,052 였다. 복권은 1달러 이므로 모두 700만 달러였으나 1등 당첨금은 2,700만 달러였다. 1장당 당첨금의 기댓값은 3.8달러 이므로 비용 1달러를 크게 웃돈다. (통계와 확률의 원리, 2017)
네이만은 말년에 했던 인터뷰에서, 1950년대 국제회의에서 프랑스어로 논문을 발표했을 때를 이야기 했다. 그가 단상으로 올라갔을때 청중에서 피셔를 발견했고, 논문을 발표하는 동안 앞으로 받게 될 공격에 대해 단단히 마음 먹고 있었다. 네이만이 발표를 끝내고 청중들로부터 질문을 기다렸다. 피셔는 아무 말도 하지 않았다. 나중에 네이만은 피셔가 프랑스어를 하지 못한다는 사실을 알게 됐다. (p131 차를 맛보는 여인 2001, 2019)
Last Modified: 2022/02/18 18:33:05



