Activation, Cost Functions
Activation Functions
- ReLU, He 초기값(표준편차 \({\sqrt{\frac{n}{2}}}\)), 편향(b)은 0으로 초기화하는게 일반적이다. 1
- Sigmoid \({\sigma}(x)=\frac{1}{1+e^{-x}}\) Xavier 초기값(표준편차 \({\frac{1}{\sqrt{n}}}\))
- \(tanh(x)=2{\sigma}(2x)-1\) tanch, 시그모이드로 간단히 표현할 수 있다.
- 시그모이드와 달리 함수값이 zero-centered 되어 있다.
세상에서 가장 중요한 곡선: 시그모이드
헤밍웨이의 소설 『태양은 다시 떠오른다』에서 마이크 켐벨은 어떻게 파산했느냐는 질문에 간단히 대답한다. “두가지 상황이 있었다. 서서히 그러다가 갑자기 파산했다.” 미래학자 폴 사포는 S자 곡선 찾기로 미래를 예측한다. 당신이 샤워기 물의 온도를 딱 맞추지 못할 때, 즉 처음에는 너무 차갑다가 너무 뜨겁게 바뀔 때는 S자 곡선을 탓하라.
p.183 『마스터 알고리즘』 2015, 2016
시그모이드의 초기값에 대해,
- 표준편차stddev 1 정규분포: 활성화값 0,1에 다가감. 기울기 소실 발생
- 표준편차 0.01 정규분포: 가운데 몰림. 값이 치우치므로 표현력에 문제
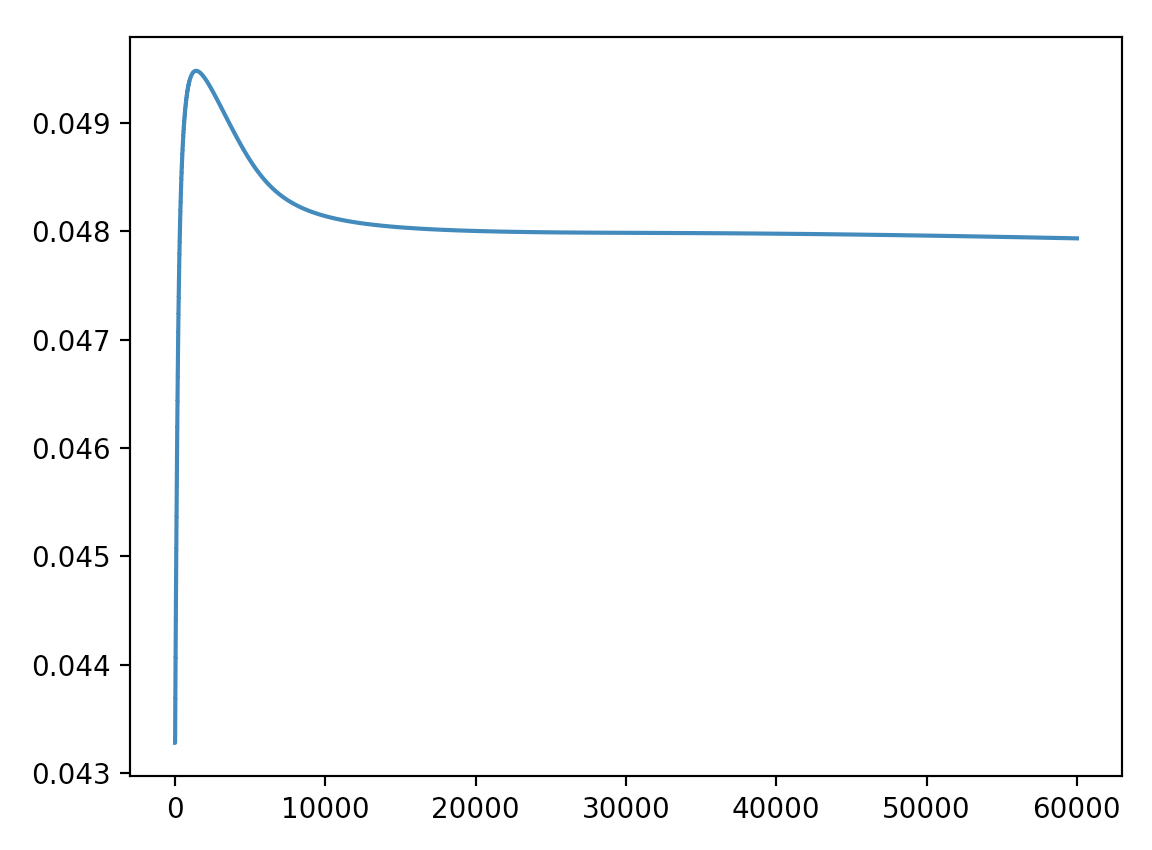
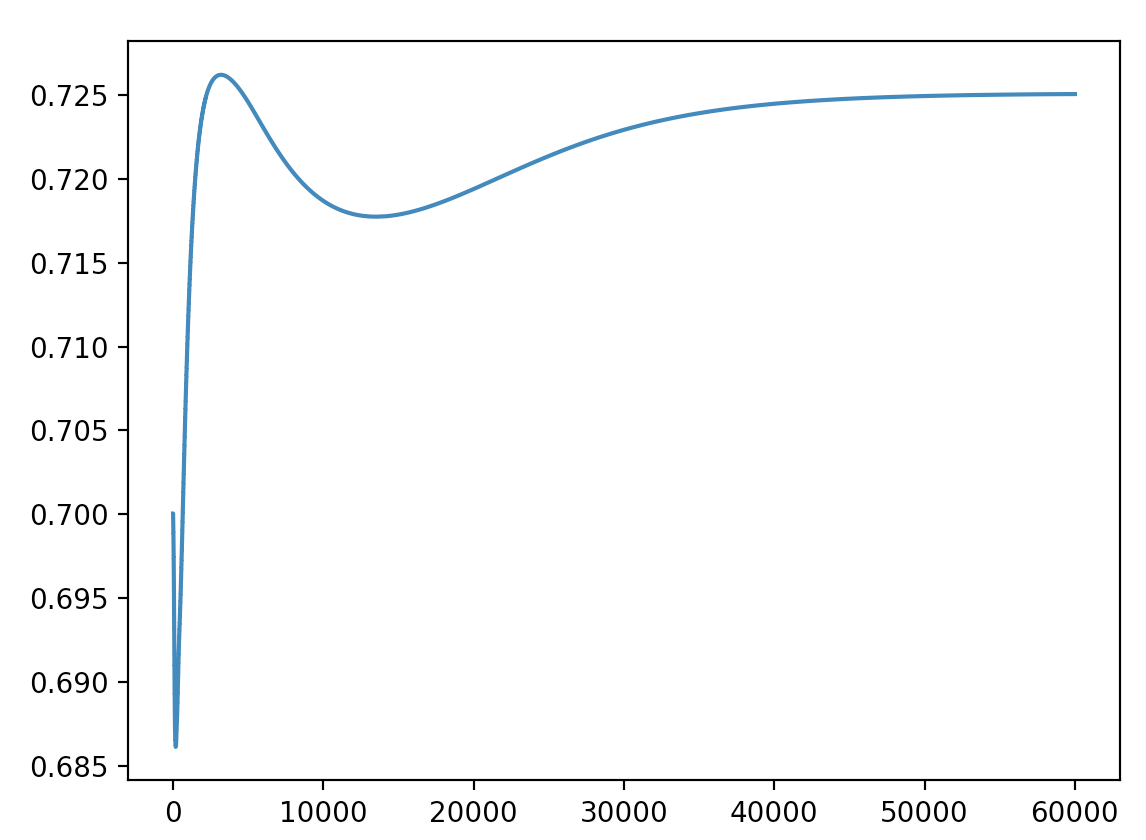
SGD로 각각 두 번 학습한 a_57(임의의 노드)의 시그모이드 활성화값 그래프
sigmoid, relu 테스트
MNIST에 대해 두 개의 은닉층에 대한 활성화 함수 유/무에 따른 loss/acc를 테스트한 결과는 다음과 같다.
| h1 | h2 | loss / acc | 비고 |
|---|---|---|---|
| n/a | n/a | 0.213/0.9164 | 학습 안됨 |
| n/a | sigmoid | 0.054/0.972 | 마지막에 학습이 잘 안됨 |
| n/a | relu | 0.027/0.977 | 마지막에 학습이 잘 안됨 |
| sigmoid | n/a | 0.008/0.980 | |
| sigmoid | sigmoid | 0.000/0.9812 | 레이어가 깊어진다면 sigmoid는 vanishing gradient가 발생할듯 |
| sigmoid | relu | 0.000/0.9842 | |
| relu | n/a | 0.000/0.9779 | |
| relu | sigmoid | 0.001/0.9822 | |
| relu | relu | 0.001/0.984 |
softmax
아래 매트릭스의 [1,1]의 Softmax는 0.08761067으로 계산 결과는 아래와 같다.

\(e\)를 밑으로 하는 Softmax는 기본 값이나 제곱에 비해 평균을 기준으로 변동폭이 크다. (빨간색)

Cost Functions
Cost/Loss/Error 모두 같은 의미로 쓰인다.
Cross Entropy Error
Regression에는 SSE가 사용되고 멀티클래스 분류에는 Cross Entropy Error를 사용한다. 출력층을 Softmax로 하고 총합은 항상 1이 된다.
멀티클래스 분류에도 이진 분류와 같이 신경망이 구현하는 함수를 각 클래스의 사후확률에 대한 함수로 간주하고, 그러한 확률 모형을 기반으로 훈련 데이터에 대한 신경망 파라미터의 우도를 평가하여 그 우도를 최대화한다. 이 우도에 로그를 취하여 부호를 반전한 것을 오차 함수로 삼는다. (딥러닝 제대로 시작하기, 2015)
\[E=-{\sum_{k}t_k{\log{y_k}}}\]Entropy는 Decision Tree를 ID3로 구현할때도 사용한다.
relative entropy
= cross entropy
= kullback-leibler divergence
완전히 똑같은 두 함수의 relative entropy는 0이다.
For discrete p and q this means:
(위키피디어)
Softmax의 Cross Entropy Error 코드는 아래와 같이 정의했다.
# Y = one-hot vector
# y = softmaxed value
cost = - tf.reduce_mean(tf.reduce_sum(Y * tf.log(y), axis=1))
softmax의 cross-entropy는 아래 설명하는 LogSumExp 패턴이 나타난다.

Tricks of the Trade: LogSumExp
읽을 것
Keras’ Loss functions
mean_squared_error
SSE는 Sum of Squared Errors이며 따라서 \(MSE={\frac{1}{n}}{\times}SSE\) 이다.
앤드류 응 머신러닝 강좌를 보면 Cost Function으로 MSE의 1/2을 취하는데 이에 대한 자세한 소개. 미분시 상수항이 떨어지므로 계산을 쉽게 하기 위함이며 MSE 앞에 One Half를 붙인 One Half Mean Squared Error로 부른다.
mean_absolute_error
Computing the sum of absolutes (MAE) corresponds to the ℓ1 norm, noted ∥ · ∥1. It is sometimes called the Manhattan norm because it measures the distance between two points in a city if you can only travel along orthogonal city blocks. (Hands-On Machine Learning with Scikit-Learn and TensorFlow, 2017)
categorical_crossentropy
If it is a multiclass(or multi-label) problem, you have to use categorical_crossentropy.
Keras의 categorical_crossentropy는 tf에서 tf.nn.softmax_cross_entropy_with_logits를 실행하고, binary_crossentropy는 tf.nn.sigmoid_cross_entropy_with_logits를 실행한다.
신경망 성능 개선을 보면 cost function으로 cross entropy를 사용할때 성능이 매우 좋은 것을 확인할 수 있다.
binary_crossentropy
binary classification에 대해서만 사용한다. negative를 위 수식처럼 1-true로 함께 학습한다. multi class에서 사용한다고 전체 negative에 대해 학습하는 수식은 아니므로 주의가 필요하다.
참고
binary crossentropy 그래프. 당연히 5:5로 구분될때 엔트로피가 1로 가장 높고, 한쪽으로 쏠리면 0이 된다.

기타 함수
LogSumExp
LSE는 머신러닝 알고리즘에 주로 사용되는 부드러운 근사값 형태의 maximum function(≈ max())이다.
>>> from scipy.special import logsumexp
>>> a = np.arange(10)
>>> np.log(np.sum(np.exp(a)))
9.4586297444267107
>>> logsumexp(a)
9.4586297444267107
max 값 기준으로 하위값 변동에 큰 영향을 받지 않으며 max 보다 조금 더 큰 부드러운 값을 나타낸다.

Last Modified: 2021/06/08 13:03:45





