Decision Tree

개요
- ID3
- CART
Random Forest
Gradient Boosting
- Adaboost
- C5.0

개요

One model for performing decision tree analysis was created by J. Ross Quinlan at the University of Sydney and presented in his book Machine Learning, vol.1, no. 1, in ~~1975~~ (10). His first algorithm for decision tree creation was called the Iterative Dichotomiser 3 (ID3). (A Brief History of Decision Tree Analysis)

책 출간 연도가 1975로 되어 있는데, 책 정보에 따르면 1986년이 맞다. (책 본문 PDF) 위키피디어에도 1986으로 기입되어 있다. Quinlan은 첫 ID3 이후 C4.5(1993), C5.0 상업적 모델로 발전 시켰다. C5.0은 책 『Applied Predictive Modeling』에도 나온다. 번역서는 『실전 예측 분석 모델링』 CART 부터 C4.5, PART등을 다룬다. p.429 ~ 446

테러리스트 구분에 Decision Trees를 사용했다. 신용카드 사기 검출과 얼굴 인식에는 신경망을 이용했다. (넘버스 2017)

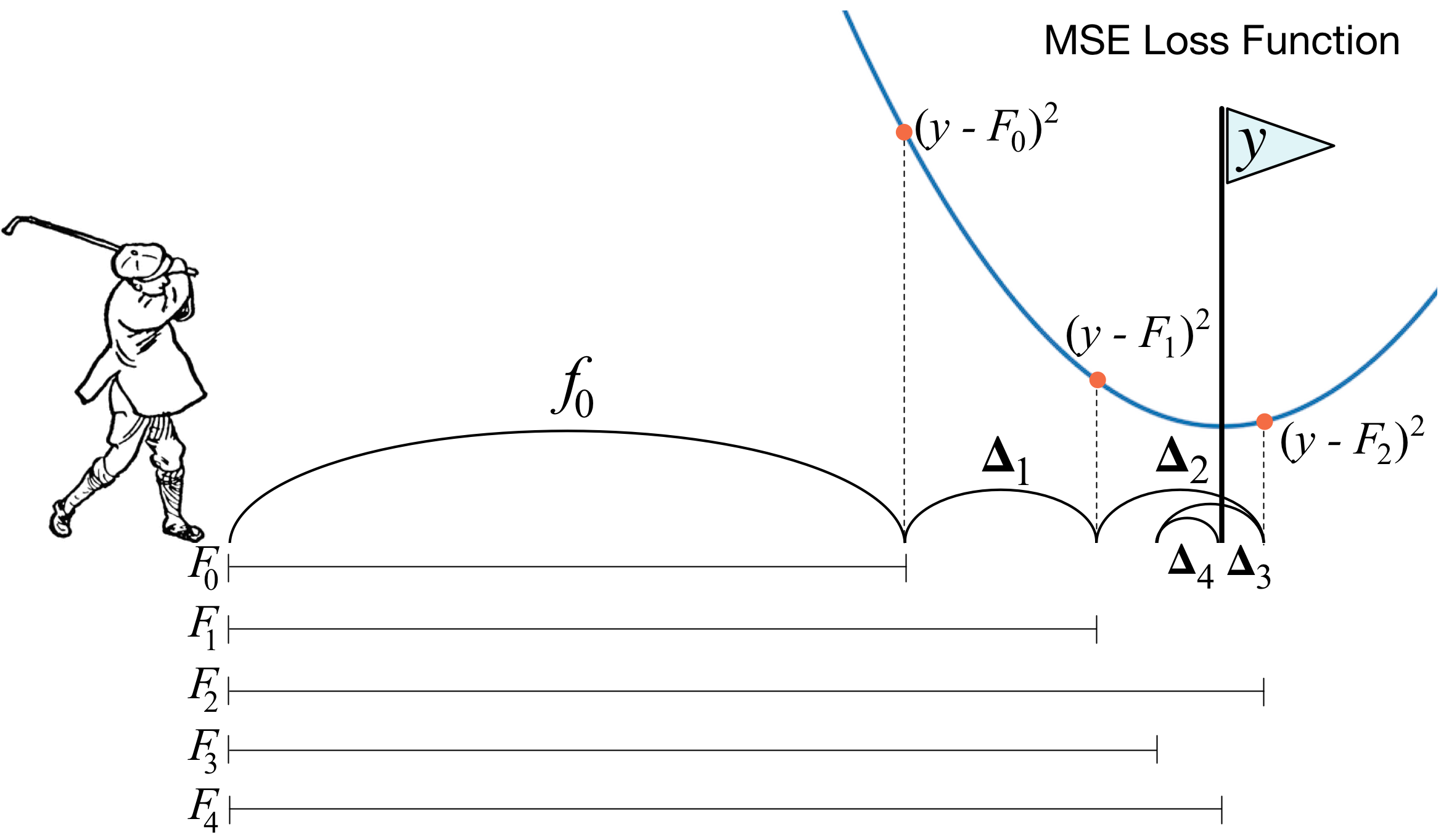
노드에 포함된 모든 example들이 원하는 y값에 대해 같은 y값을 가지고 있을때 pure하다.

Iris 분류를 if else 룰로 표현한다면 아래와 같은 형태가 된다.

(데이터 마이닝 Data Mining, 2011, 2013, p.60)

ID3

ID3, C4.5에서는 Entropy를 기준으로 하는 Information gain을 사용한다. (Regression은 calculate_variance_reduction)

information gain is a synonym for Kullback–Leibler divergence (Wikipedia)

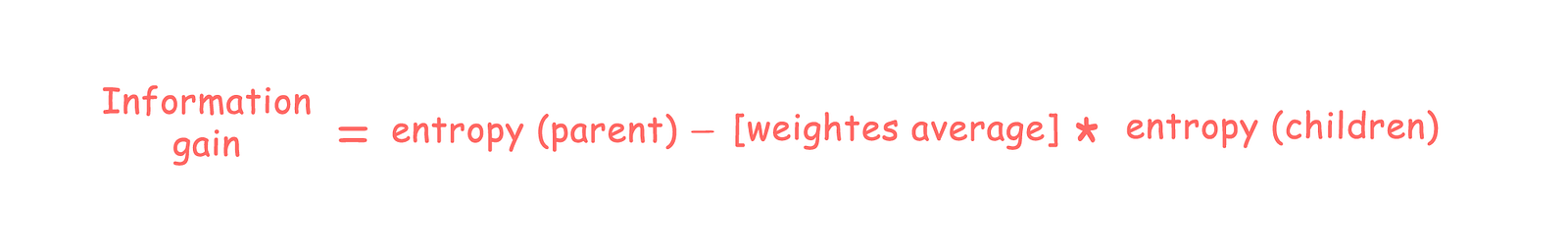(What is Entropy and why Information gain matter in Decision Trees?)

(ID3 수도 코드와 선행 지식, ID3 코드 구현)

CART

CART 알고리즘에서는(scikit-learn은 CART를 최적화한 알고리즘 사용) Gini impurity를 디폴트로 사용한다. Not to be confused with Gini coefficient. CART는 greedy 알고리즘이다. ID3도 동일. CART는 Leo Breiman et. al(1984) (Who invented the decision tree?)

\[\textit{Gini}: \mathit{Gini}(E) = 1 - \sum_{j=1}^{c}p_j^2\] \[\textit{Entropy}: H(E) = -\sum_{j=1}^{c}p_j\log p_j\]

수식대로 계산해보면 균등하게 분류될수록 Gini impurity가 높다. 한쪽으로 쏠릴 수록 Gini impurity가 낮다. e.g. {0.5, 0.5} = 0.5, {0.1, 0.9} = 0.18. A perfect separation results in a Gini score of 0. 기본적으로 Gini impurity와 Entropy는 동일한 패턴을 보인다.

Random Forest

넷플릭스 프라이즈의 우승자는 머신러닝 알고리즘 수백 가지를 통합한 메타학습 알고리즘을 사용했다. 왓슨은 메타학습 알고리즘을 사용해 후보로 올라온 대답들 중에서 최종 대답을 선택했다. 이런 종류의 메타학습을 스택킹 ^stacking이라 부르며 ‘세상에 공짜는 없다’라는 정리의 창시자 데이비드 월퍼트가 생각해낸 방식이다. 이보다 훨씬 더 간단한 메타학습은 통계학자 레오 브라이먼^{Leo Breiman et al., 2001}이 발명한 배깅 ^bagging이 있다. 배깅은 여러 학습 예제를 무작위로 만들어 알고리즘에 적용 후 그 결과들을 투표 방식으로 통합한다. 이렇게 하는 까닭은 분산이 줄어들기 때문이다. 배깅은 데이터가 예상 밖의 변화가 생겼을때 단일 모델보다 훨씬 덜 민감하므로 정확도를 향상하는 매우 쉬운 방법이다. 키넥트는 랜덤 포레스트를 사용한다.
p.384 『마스터 알고리즘』 _{2015, 2016}

Bagging Trees

b=1…B random sampling
tree 구성(e.g. ID3)
classification B개 모든 tree를 사용해서 분류, majority vote로 결정.

특징은 아래와 같다.

can induce non-linear decision boundaries.
fast at prediction(O(height of tree))

Iris의 0:1 features로 rf 분류, 정확도 0.96667 모델 decision boundaries(mlxtend)이다.

Gradient Boosting

학습이론가 요아브 프로인트 ^{Yoav Freund}와 롭 샤피르 ^{Rob Schapire}가 발명한 부스팅 ^boosting이 있다. 부스팅은 여러 학습 알고리즘을 결합하는 대신 이전 모형들이 저지른 실수를 바로잡는 새 모형을 이용하면서 같은 분류기를 데이터에 반복 적용한다. 학습을 할 때마다 잘못 분류한 사례의 가중치를 증가시켜 다음번 학습에서는 이 사례에 더욱 집중하도록 한다. 부스팅이라는 이름은 이 과정이 처음에는 무작위 추측보다 그저 약간 좋기만 한 분류기를 지속적으로 강화하여 거의 완전한 분류기로 만든다는 개념에서 나왔다.
p.384 『마스터 알고리즘』 _{2015, 2016}

CrossEntroy loss의 gradient를 구하고 이를 다시 학습, update * learning_rate를 반영한 다음 다시 loss를 구해 estimators 만큼 반복한다. 결국 residual errors를 반복 학습한다.

for i in self.bar(range(self.n_estimators)):
    gradient = self.loss.gradient(y, y_pred)
    self.trees[i].fit(X, gradient)
    # XGBoost의 경우
    # self.trees[i].fit(X, y_and_pred)
    update = self.trees[i].predict(X)
    y_pred -= np.multiply(self.learning_rate, update)

predict시 \(y_{pred}\)에 대해 확률 분포(softmax)를 만들고, argmax를 택한다.

y_pred = np.exp(y_pred) / np.expand_dims(np.sum(np.exp(y_pred), axis=1), axis=1)
# XGBoost의 경우
# y_pred = np.exp(y_pred) / np.sum(np.exp(y_pred), axis=1, keepdims=True)
y_pred = np.argmax(y_pred, axis=1)
return y_pred

Adaboost

(Yoav Freund and Robert Schapire, 2003)

부스팅은 모든 분류 기법에 적용할 수 있지만, 트리의 가지를 거의 두지 않음으로써 트리 깊이에 제약을 두어 약 분류기로 만들 수 있기 때문에 분류 트리를 가장 많이 쓴다. 브레이먼(1998)은 부스팅에 왜 분류 트리가 적합한지를 설명했다. 분류 트리는 편향성이 낮고, 분산이 높은 기법으로 트리 앙상블을 통해 분산을 낮출 수 있으므로 그 결과 편향성과 분산 모두 낮은 결과를 구한다. (p.451 실전 예측 분석 모델링, 2013, 2018)

C5.0

C5.0은 퀸란이 C4.5 분류 모델에 부스팅이나 각 오차별로 각각 다른 비용을 매기는 방식 등의 기능을 추가해서 개선한 버전이다.

(실전 예측 분석 모델링, 2013, 2018)

여기서는 C5.0의 테스트셋 점수가 가장 높다.

https://explained.ai/gradient-boosting/descent.html ↩

Last Modified: 2021/06/08 13:03:45
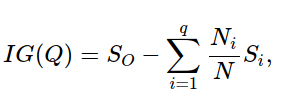