Naive Bayes

• Bayes’ theorem(Bayes’ rule)
  • 결합 확률^{joint probabilities}
  • 조건부 확률^{conditional probability}
  • 계산
• “naive” means
• 나이브 베이즈가 성공적인 이유

Bayes’ theorem(Bayes’ rule)

나이브 베이즈 알고리즘 확률 모델 문서로 정리했다.

• P(A|B) posterior 사후 확률
• P(B|A) likelihood 가능도, 우도, 조건부 확률
• P(B) evidence 증거
• P(A) prior 사전 확률

라플라스는 해가 n번 떠오른 후 다시 떠오르는 확률을 (n+1)/(n+2)로 추정하는 연속성의 규칙을 이끌어냈다.
p.243 『마스터 알고리즘』 _{2015, 2016}

결합 확률^{joint probabilities}

\(P(A,B)=P(A\bigcap{B})=P(A|B)P(B)\)

결합 사건 A와 B의 확률은 위와 같이 곱하기 법칙^{product rule}이라고도 부른다.

조건부 확률^{conditional probability}

\(P(A|B)=\frac{P(A,B)}{P(B)}\)

P(B) > 0 이어야 한다.

계산

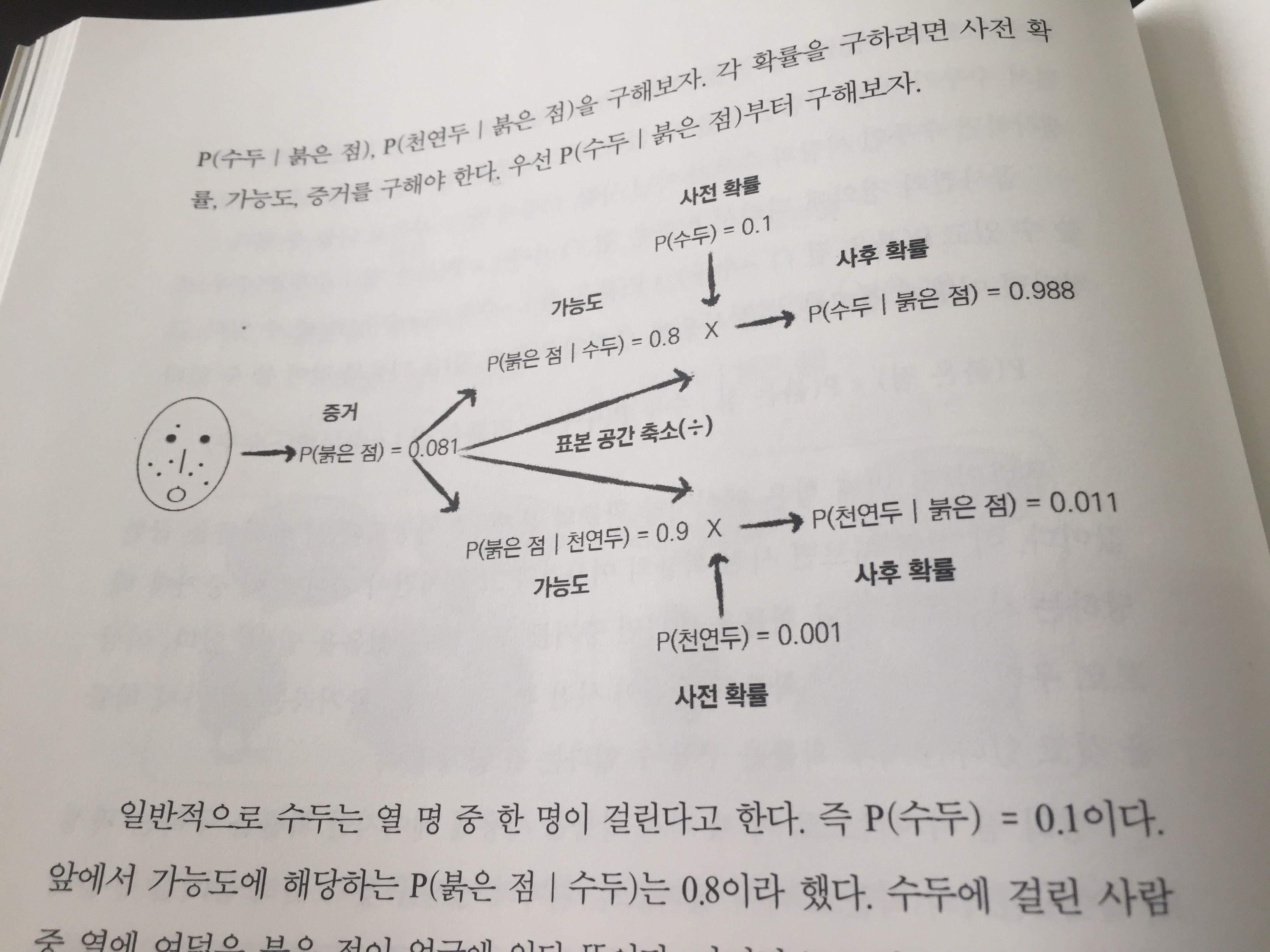
사후 확률 오즈 posterior odds^승산 R = P(수두|붉은점) / P(천연두|붉은점) = 0.988/0.011 = 90 일반적으로 3보다 크거나 1/3보다 작을 때 두 가설이 의미 있는 차이가 있다고 본다. (확률적 프로그래밍 기초 원리, 2015)

“naive” means

In simple terms, a naive Bayes classifier assumes that the presence (or absence) of a particular feature of a class is unrelated to the presence (or absence) of any other feature, given the class variable. For example, a fruit may be considered to be an apple if it is red, round, and about 4” in diameter. Even if these features depend on each other or upon the existence of the other features, a naive Bayes classifier considers all of these properties to independently contribute to the probability that this fruit is an apple.

(What is “naive” in a naive Bayes classifier?)

나이브 베이즈가 성공적인 이유

논문(Domingos, Pazzani, 1997)에서 나이브 베이즈가 성공적인 이유는 사후 확률의 우수함이 아니라 argmax_y P(Y|X)의 우수함 때문이라 말한다. 심지어 Y를 최대화하기 위한 목적에서 베이즈 룰의 사용을 피할 수 있는데, 이는 교정되지 않은 우도를 교정되지 않은 사후 확률로만 변형하기 때문이다. (머신 러닝, 피처 플래치, 2012) 이 논문의 1저자인 Domingos는 『마스터 알고리즘』을 쓴 페드로 도밍고스 교수다.

Last Modified: 2021/06/08 13:03:45